IT初心者のための アルゴリズムとデータ構造入門 ~ 基本情報ではじめるコンピュータ科学の基礎理論(4)

この連載は、これから IT の勉強をはじめる人を対象としたものです。 基本情報技術者試験の出題分野ごとに、仕組み、主要な用語、および過去問題を紹介します。 受験対策としてだけでなく、 IT の基礎知識を幅広く得るために、ぜひお読みください。
今回は、「コンピュータ科学の基礎理論」その 4 として「 アルゴリズムとデータ構造 」の分野を取り上げます。
もくじ
アルゴリズムとデータ構造が必要な理由
筆者が若かりし頃、プログラマなら必ず読んでおくべき名著として「アルゴリズム + データ構造 = プログラム」( Niklaus Wirth 著、片山卓也訳、日本コンピュータ協会発行、科学技術出版社発売、1979 年)がありました。 この本のタイトルは、プログラムの内容がアルゴリズムとデータ構造であることを示しています。
業務や趣味などで IT を活用するには、そのためのプログラムを作ることになります。
プログラムは、何らかのプログラミング言語で記述された文書ですが、その内容は、アルゴリズムとデータ構造なのです。
したがって、プログラムを作るには、アルゴリズムとデータ構造を見出さなければなりません。これが、アルゴリズムとデータ構造が必要な理由です。
アルゴリズムとは? データ構造とは?
アルゴリズムとは、与えられた問題を解く(プログラムで実現する)ための明確な手順のことです。 データ構造とは、その手順の中で使われるデータのことです。
たとえば、「 100 人の学生の身長の平均値を求める」というプログラムを作るとしましょう。
このプログラムのアルゴリズムは、以下の通りです。
- 100 人の学生の身長を入力する
- 身長の平均値を計算する
- 身長の平均値を出力する
このプログラムのデータ構造は、 100 人の学生の身長を格納する配列と、平均値を格納する変数です(図 1 )。
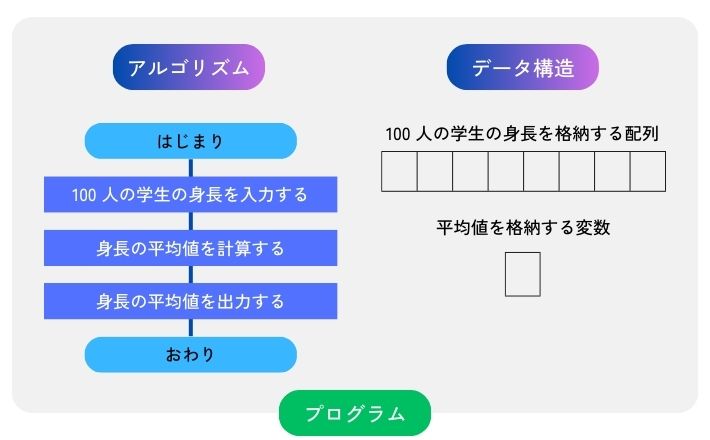
このように、アルゴリズムとデータ構造を見出せるのは、すぐ後で説明する基本的なアルゴリズムとデータ構造を知っているからです。
覚えておくべき基本的なアルゴリズムとデータ構造
アルゴリズムとデータ構造は、自分で見出すものですが、覚えておくべき基本的なアルゴリズムとデータ構造というものがあります。 これらは、様々な場面で利用できるものです。さらに、これらを知ることで、発想の幅が広がり、より自由な発想ができるようになります。
基本情報技術者試験のシラバス(知識・技能の細目)には、覚えておくべき基本的なアルゴリズムとデータ構造が示されています(図 2 )。
図 2 シラバスに示された基本的なアルゴリズムとデータ構造(主要なものだけを抜粋)
-
アルゴリズム
- 整列のアルゴリズム
- バブルソート
- 選択ソート
- 挿入ソート
- マージソート
- クイックソート
- 探索のアルゴリズム
- 線形探索
- 二分探索
- ハッシュ表探索法
-
データ構造
- 配列
- 配列
- 二次元配列
- リスト
- 単方向リスト
- 双方向リスト
- 循環リスト
- バッファ
- キュー
- スタック
- 木(ツリー)
- 二分探索木
- ヒープ
整列(ソート)のアルゴリズムは、配列を昇順や降順に並べ替えます。
探索(サーチ)のアルゴリズムは、配列の中から目的のデータを見つけます。
整列と探索それぞれに複数のアルゴリズムがあるのは、状況に応じて使い分けるためです。
-
例
- 探索の対象となる配列がランダム(整列されていない)なら …
- arrow_forward 線形探索のアルゴリズムを使います
- 配列が整列されているなら …
- arrow_forward 二分探索のアルゴリズムを使います
データ構造の基本は、複数のデータが一直線に並んだ配列です。 他のデータ構造は、配列の読み書きにルールを設けることで実現されます。
- リストは、つながり情報(ポインタとも呼びます)を持った配列です
- バッファは、データを一時的に格納する配列です
- 木は、2つのつながり情報を持った配列であり、データが木のように枝分かれしてつながります
基本的なアルゴリズムとデータ構造を習得するには、それらを手作業でやってみるとよいでしょう。
トランプ(もしくは数字を書いた紙)を使えば、整列や探索ができます。 トランプを一直線に並べれば、配列のデータ構造を表せます。 トランプを枝分かれするように配置すれば、二分探索木やヒープのデータ構造を表せます。
info_outlineトランプで二分探索法を再現

アルゴリズムとデータ構造の過去問題
アルゴリズムとデータ構造の過去問題を 3 問ほど紹介しましょう。
整列のアルゴリズムに関する問題
最初は、整列のアルゴリズムに関する問題です。
手作業でやったことがあれば、選択肢が何のアルゴリズムを説明しているかがわかるでしょう。
問 6 平成 30 年度 秋期
クイックソートの処理方法を説明したものはどれか。
- ア
- 既に整列済みのデータ列の正しい位置に,データを追加する操作を繰り返していく方法である。
- イ
- データ中の最小値を求め,次にそれを除いた部分の中から最小値を求める。 この操作を繰り返していく方法である。
- ウ
- 適当な基準値を選び,それより小さな値のグループと大きな値のグループにデータを分割する。同様にして,グループの中で基準値を選び,それぞれのグループを分割する。 この操作を繰り返していく方法である。
- エ
- 隣り合ったデータの比較と入替えを繰り返すことによって,小さな値のデータを次第に端のほうに移していく方法である。
解説
- ア
- 「既に整列済みのデータ列にデータを追加する(挿入する)」なので、挿入ソートの説明です。
- イ
- 「データ中の最小値を求める(選択する)」なので、選択ソートの説明です。
- ウ
- 「基準値を選んでグループに分割する」なので、クイックソートの説明です。
- エ
- 「隣り合ったデータの比較と入れ替え(交換)」なので、バブルソート(交換法とも呼びます)の説明です。
ここでは、クイックソートの処理方法を選ぶので、選択肢ウが正解です。
解答 ウ
探索のアルゴリズムに関する問題
次は、探索のアルゴリズムに関する問題です。
探索には、いくつかのアルゴリズムがありますが、それらを状況に応じて使い分けることに注目してください。
2 分探索に関する記述のうち,適切なものはどれか。
- ア
- 2 分探索するデータ列は整列されている必要がある。
- イ
- 2 分探索は線形探索より常に速く探索できる。
- ウ
- 2 分探索は探索をデータ列の先頭から開始する。
- エ
- n 個のデータの探索に要する比較回数は, nlog2n に比例する。
解説
- ア
- 二分探索法は、整列された配列を対象とした探索のアルゴリズムなので、選択肢アは適切です。
- イ
- 二分探索法は、線形探索法より効率的にデータが見つかるアルゴリズムですが、常に線形探索法より速いとは限りません。
たとえば、配列の先頭に目的のデータがある場合は、二分探索法より線形探索法の方が、速くデータが見つかります。 したがって、選択肢イは不適切です。 - ウ
- 二分探索法は、整列された配列の真ん中の要素をチェックすることを繰り返します。 したがって、選択肢ウは不適切です。 配列の先頭から探索を開始するのは、線形探索法です。
- エ
- 要素数 n 個の配列を二分探索するときの比較回数は、 log2n (この式は、 n 個の要素を 2 分割して最後の 1 つになるまでの処理回数を意味します)に比例します。 したがって、選択肢エは不適切です。
以上のことから、選択肢アが正解です。
解答 ア
二分探索木のデータ構造に関する問題
最後は、二分探索木のデータ構造に関する問題です。
手作業で二分探索木を作ったことがあれば、選択肢に示された図が二分探索木かどうかを判断できるでしょう。
問 5 平成 31 年度 春期
2 分探索木として適切なものはどれか。 ここで, 1 ~ 9 の数字は,各ノード(節)の値を表す。
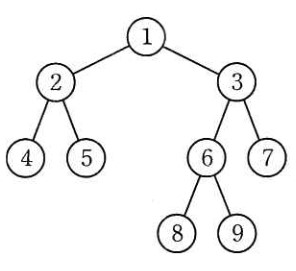
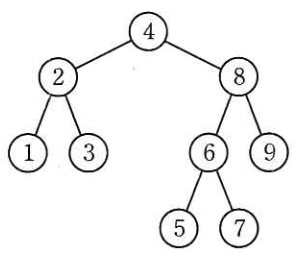
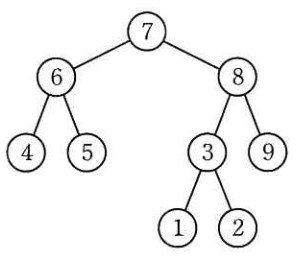
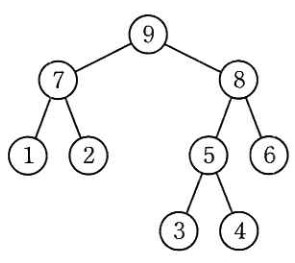
解説
木のデータ構造を図に示すときは、多くの場合に、要素(この問題では、ノード(節)と呼んでいます。 個々の要素は、木の節に相当するものだからです)を、四角形ではなく円で表します。 二分探索木は、より小さい要素を左側に、より大きい要素を右側につないだものです。
- ア
- ② の左側に、 ② より大きな ④ があるので、二分探索木ではありません(他にも不適切な部分があります)。
- イ
- どの要素も、より小さい要素が左側、より大きい要素が右側になっているので、二分探索木です。
- ウ
- ③ の右側に、 ③ より小さな ② があるので、二分探索木ではありません。
- エ
- ⑦ の右側に、 ⑦ より小さな ② があるので、二分探索木ではありません(他にも不適切な部分があります)。
以上のことから、選択肢イが正解です。
解答 イ
今回は、「基礎理論」その 4 として「アルゴリズムとデータ構造」の分野から、アルゴリズムとデータ構造が必要な理由、覚えておくべき基本的なアルゴリズムとデータ構造、およびアルゴリズムとデータ構造の過去問題を紹介しました。
この連載は、今回で最終回です。
これまで記事をお読みいただいた皆様に、この場をお借りして、厚く御礼申し上げます。
それでは、またどこかで、お会いしましょう!
label 関連タグ免除試験を受けた 74.9% の方が、科目A免除資格を得ています。
※独習ゼミは、受験ナビ運営のSEプラスによる試験対策eラーニングです。

IT初心者のための アルゴリズムとデータ構造入門 ~ 基本情報ではじめるコンピュータ科学の基礎理論(4)
update
IT初心者のための 論理回路 入門 ~ 基本情報ではじめるコンピュータ科学の基礎理論(3)
update
IT初心者のための 2進数 入門 ~ 基本情報ではじめるコンピュータ科学の基礎理論(2)
update
IT初心者のための基本情報ではじめる ストラテジ 入門
update
IT初心者のための基本情報ではじめる サービスマネジメント 入門 ~マネジメント分野 2
update
IT初心者のための基本情報ではじめる プロジェクトマネジメント 入門 ~マネジメント分野 1
update
IT初心者のための基本情報ではじめる 開発技術 入門
update
IT初心者のための基本情報ではじめる 暗号化 入門 ~セキュリティ分野 2
update
IT初心者のための基本情報ではじめる セキュリティ 入門 ~セキュリティ分野 1
update
IT初心者のための基本情報ではじめる OSI基本参照モデル 入門 ~ネットワーク分野 2
update
『プログラムはなぜ動くのか』(日経BP)が大ベストセラー
IT技術を楽しく・分かりやすく教える“自称ソフトウェア芸人”
大手電気メーカーでPCの製造、ソフトハウスでプログラマを経験。独立後、現在はアプリケーションの開発と販売に従事。その傍ら、書籍・雑誌の執筆、またセミナー講師として活躍。軽快な口調で、知識0ベースのITエンジニアや一般書店フェアなどの一般的なPCユーザの講習ではダントツの評価。
お客様の満足を何よりも大切にし、わかりやすい、のせるのが上手い自称ソフトウェア芸人。
主な著作物
- 「プログラムはなぜ動くのか」(日経BP)
- 「コンピュータはなぜ動くのか」(日経BP)
- 「出るとこだけ! 基本情報技術者」 (翔泳社)
- 「ベテランが丁寧に教えてくれる ハードウェアの知識と実務」(翔泳社)
- 「ifとelseの思考術」(ソフトバンククリエイティブ) など多数










