稼働率の計算方法がわかる|かんたん計算問題

この連載では、基本情報技術者試験で、多くの受験者が苦手意識を持っている「計算問題」に的を絞って、計算方法を詳しく説明します。苦手克服のポイントは、身近な具体例で、計算方法のイメージをつかむことです。
丸暗記ではなく、感覚的に理解してください。そうすれば、様々な問題に応用できます。
今回のテーマは、トップ 10 に入るくらいよく出る「稼働率」です。稼働率の計算方法がわかったら、いくつか過去問題を解いてみましょう。
もくじ
用語解説 稼働率とは何か?
たとえば、全体で 100 時間のうち 90 時間動作して 10 時間停止したシステムの稼働率は、以下の計算で求められ、0.9( 90% )になります。「そんなの当然じゃん!」ですね。
- 稼働率
- = 動作した時間 / 全体の時間
- = 90 時間 / 100 時間
- = 0.9( 90 % )
この稼働率の計算式を MTBF と MTTR という言葉を使って書くと、以下になります。
「うわっ、急に難しくなった!」でしょう。
でも、ご安心ください。この難しそうな式も「そんなの当然じゃん!」だからです。
MTBF は、Mean Time Between Failure(故障と故障の間の平均時間)の略であり、MTTR は、Mean Time To Repair(修理のための平均時間)の略です。
システムは必ず故障するものと考えて、故障と故障の間が「動作した時間」であり MTBF と呼び、故障して修理中の時間が「停止した時間」であり MTTR と呼ぶのです。
MTBF + MTTR は、「動作した時間+停止した時間」なので「全体の時間」ということになります。
したがって、「 稼働率 = MTBF / ( MTBF + MTTR )」という難しそうな式は、以下のように変形して、「稼働率 = 動作した時間 / 全体の時間」という簡単な式と同じになります。
- 稼働率
- = MTBF / ( MTBF + MTTR )
- = 動作した時間 / (動作した時間+停止した時間)
- = 動作した時間 / 全体の時間
システムの稼働率の計算方法(直列の場合)
システムには、様々な構成がありますが、基本となる「直列」と「並列」の稼働率の計算方法をマスターすれば、様々な構成に応用できます。
まず、直列の稼働率の計算方法です。
身近な具体例として、稼働率 0.9 のパソコン 1 台と、稼働率 0.8 のプリンタ 1 台から構成されたシステムがあるとします。
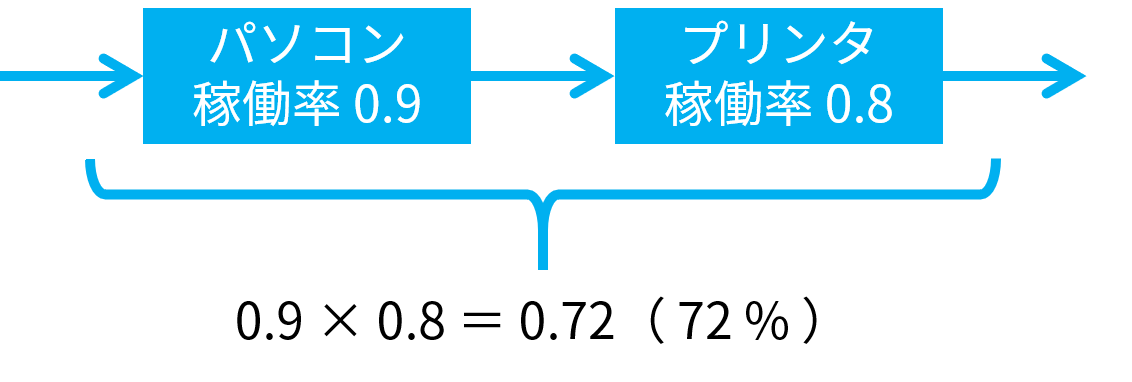
同じ役割を持つ装置が 1 台しかない場合は、直列でつながっていると考えて、以下の図で示します。装置をつなぐ矢印は、データの流れを示します。

パソコンに入ったデータは、90 % の確率でパソコンから出てきます。そのデータがプリンタに入って、90 % の 80 % の 72 % のデータがプリンタから出てきます。
したがって、システム全体の稼働率は 72 % になります。これは、以下のように、それぞれの装置の稼働率を掛けることで求められます。
システム全体の稼働率の計算方法(並列の場合)
身近な具体例として、稼働率 0.9 のサーバ A と稼働率 0.8 のサーバ B から構成されたシステムがあり、少なくともどちらが一方が動作していればサービスを提供できるとします。
同じ役割を持つ装置が複数台あり、どれか 1 台が動作していればよい場合は、並列でつながっていると考えて、以下の図で示します。
システムに入ったデータは、いずれかのサーバで処理できれば、システムから出てくることができます。

どちらか一方が動作していればよい場合、
- システム全体の稼働率
- = 1 – ( 両方の装置が同時に停止する確率 )
(この 1 は、100% という意味です)
で求めることができます。
- 両方の装置が同時に停止する確率
- = ( 一方の装置が停止する確率 ) × ( もう一方の装置が停止する確率 )
で求められます。
そして、それぞれは、
- 装置が停止する確率
- = 1 – ( 装置の稼働率 )
で求められます。
したがって、このシステムの稼働率は、以下の 1. ~ 4. の順に計算して、0.98( 98 % )になります。
- サーバ A が停止する確率
1 – 0.9 = 0.1 - サーバ B が停止する確率
1 – 0.8 = 0.2

- サーバ A とサーバ B の両方が同時に停止する確率
0.1 × 0.2 = 0.02 - サーバ A とサーバ B のいずれかが動作する確率
1 - 0.02 = 0.98( 98 % )
これがシステムの稼働率
直列と並列ぞれぞれのシステムの稼働率を求める問題
それでは、稼働率を計算する問題を解いてみましょう。
はじめは、直列と並列それぞれのシステムの稼働率を求める問題です。先ほど示した具体例を、そのまま問題にしたような内容です。
2 台の処理装置から成るシステムがある。少なくともいずれか一方が正常に動作すればよいときの稼働率と,2 台とも正常に動作しなければならないときの稼働率の差は幾らか。ここで,処理装置の稼働率はいずれも 0.9 とし,処理装置以外の要因は考慮しないものとする。
ア 0.09 イ 0.10 ウ 0.18 エ 0.19
「少なくともいずれか一方が正常に動作すればよいときの稼働率」は、並列のシステムであり、以下の 1. ~ 4. の順に計算して 0.99( 99 % )になります。
- 処理装置 A が停止する確率
1 – 0.9 = 0.1 - 処理装置 B が停止する確率
1 – 0.9 = 0.1

- 処理装置 A と処理装置 B の両方が同時に停止する確率
0.1 × 0.1 = 0.01 - 処理装置 A と処理装置 B のいずれかが動作する確率
1 - 0.01 = 0.99( 99 % )
これがシステムの稼働率
「 2 台とも正常に動作しなければならないときの稼働率」は、直列のシステムであり、以下のように 0.81( 81 % )になります。
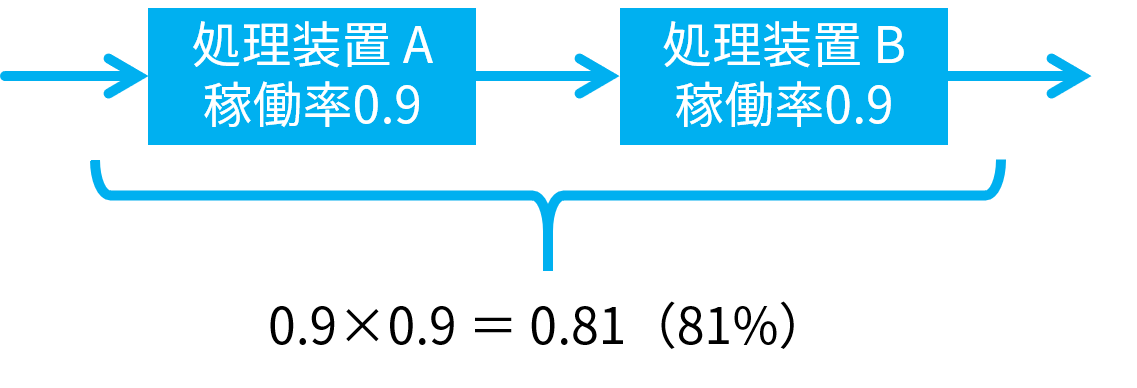
したがって、両者の差は、0.99-0.81 = 0.18( 18 % )であり、選択肢ウが正解です。
正解 ウ
直列と並列を組合せたシステムの稼働率を求める問題
今度は、直列と並列を組合せたシステムの稼働率を求める問題です。同じ役割を持つ装置が1台しかない場合は直列でつながっていると考え、同じ役割を持つ装置が複数台ある場合は直列でつながっていると考えることがポイントです。
図のように,1 台のサーバ,3 台のクライアント及び 2 台のプリンタが LAN で接続されている。このシステムはクライアントからの指示に基づいて,サーバにあるデータをプリンタに出力する。各装置の稼働率が表のとおりであるとき,このシステムの稼働率を表す計算式はどれか。ここで,クライアントは 3 台のうちどれか 1 台が稼働していればよく,プリンタは 2 台のうちどちらかが稼働していればよい。
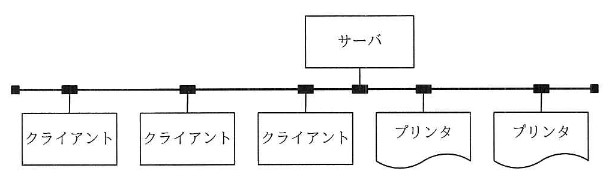
| 装置 | 稼働率 |
|---|---|
| サーバ | a |
| クライアント | b |
| プリンタ | c |
| LAN | 1 |
ア ab3c2 イ a( 1 – b3 )( 1 – c2 )
ウ a( 1 – b3 )( 1 – c )2 エ a( 1 – ( 1 – b3 )( 1 – ( 1 – c )2 )
このシステムの構成を稼働率を計算しやすい形式で示すと、以下のようになります。
1 台しかないサーバは直列で、3 台あるクライアントと 2 台あるプリンタは並列です。
稼働率 1( 100 % )の LAN は、計算に含める必要はありません。1 を掛けても、稼働率は同じだからです。
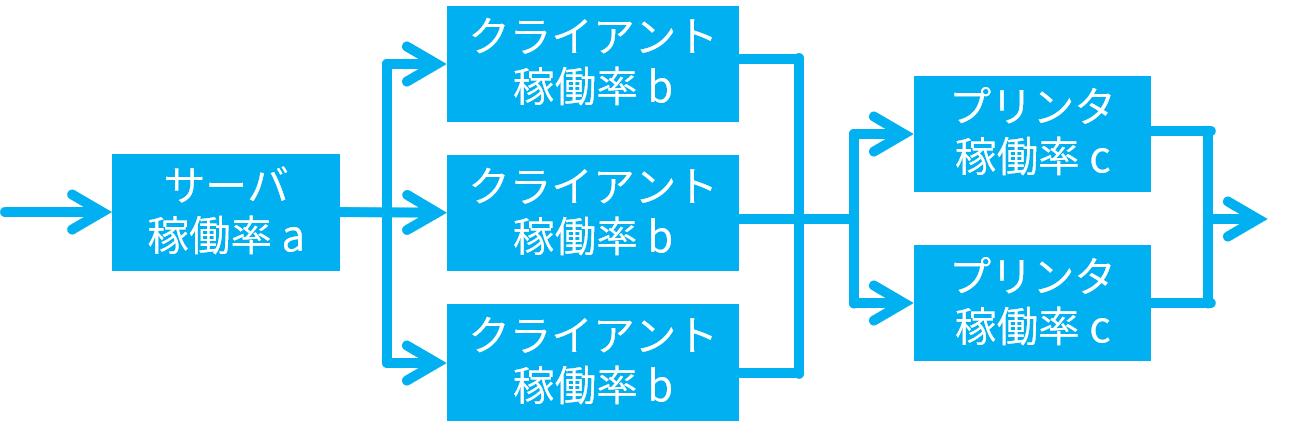
あせらずに、少しずつ計算してみましょう。
3 台あるクライアントが同時に停止する確率は、
( 1 – b ) × ( 1 – b ) × ( 1 – b ) = ( 1 – b )3
です。したがって、いずれか 1 台のクライアントが動作する確率は、 1 – ( 1 – b )3 です。
2 台あるプリンタが同時に停止する確率は、
( 1 – c ) × ( 1 – c ) = ( 1 – c )2
です。したがって、いずれか 1 台のプリンタが動作する確率は、1 – ( 1 – c )2 です。
以上のことから、このシステムは、稼働率 a のサーバ部、稼働率のクライアント部、稼働率のプリンタ部が、直列になっていると考えることができます。
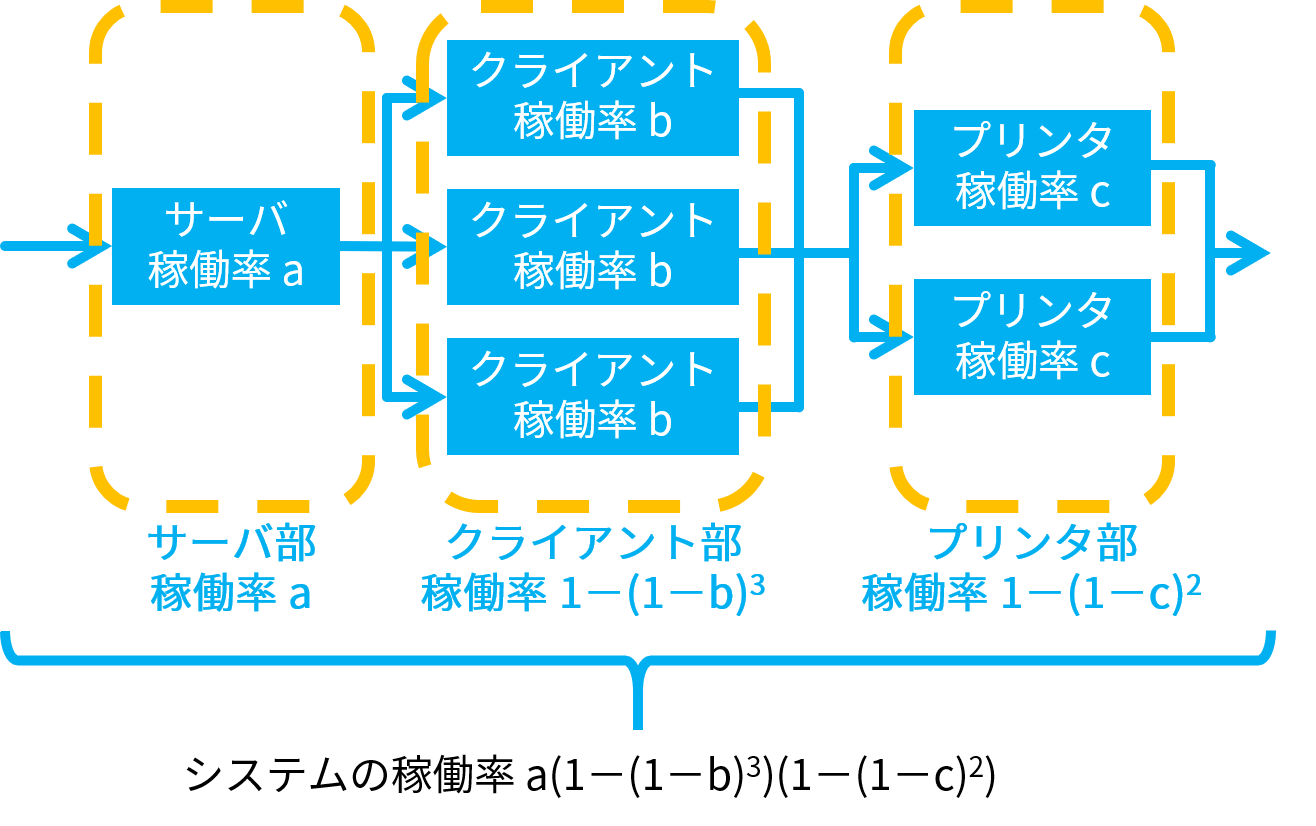
したがって、以下のようにシステムの稼働率は、それらを掛け合わせた
になり、選択肢エが正解です。
正解 エ
回線の稼働率を求める問題
今度は、回線の稼働率を求める問題です。一見して「ネットワークの問題?」と思われるかもしれませんが、稼働率を計算する問題です。
東京と福岡を結ぶ実線の回線がある。東京と福岡の間の信頼性を向上させるために,大阪を経由する破線の迂回回線を追加した。迂回回線追加後における,東京と福岡の間の稼働率は幾らか。ここで,回線の稼働率は,東京と福岡,東京と大阪,大阪と福岡の全てが 0.9 とする。
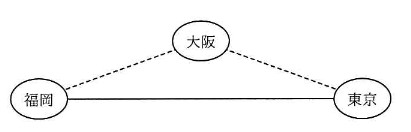
ア 0.729 イ 0.810 ウ 0.981 エ 0.999
稼働率 0.9 の回線を、これまでと同様に装置とみなせば、問題に示されたシステムの構成は、以下のようになります。
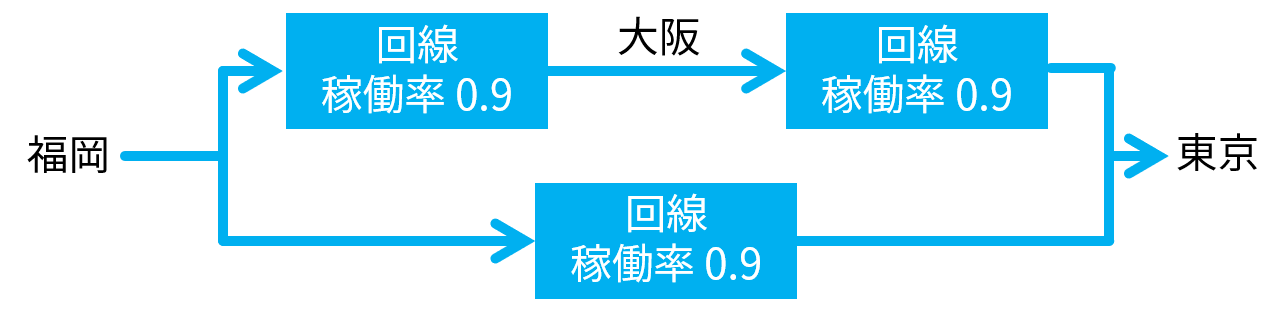
ここでも、あせらずに、少しずつ計算してみましょう。
福岡 → 大阪 → 東京の稼働率は、稼働率 0.9 の 2 台の装置が直列なので、
です。
福岡と東京の間は、この 0.81 の稼働率の部分と、もう 1 つ別の稼働率 0.9 の部分(稼働率 0.9 の装置が 1 台の部分)が並列になっています。
これらのいずれかが動作する確率(福岡と東京の間の稼働率)は、以下の (1) ~ (3) の順に計算して、0.981 になります。
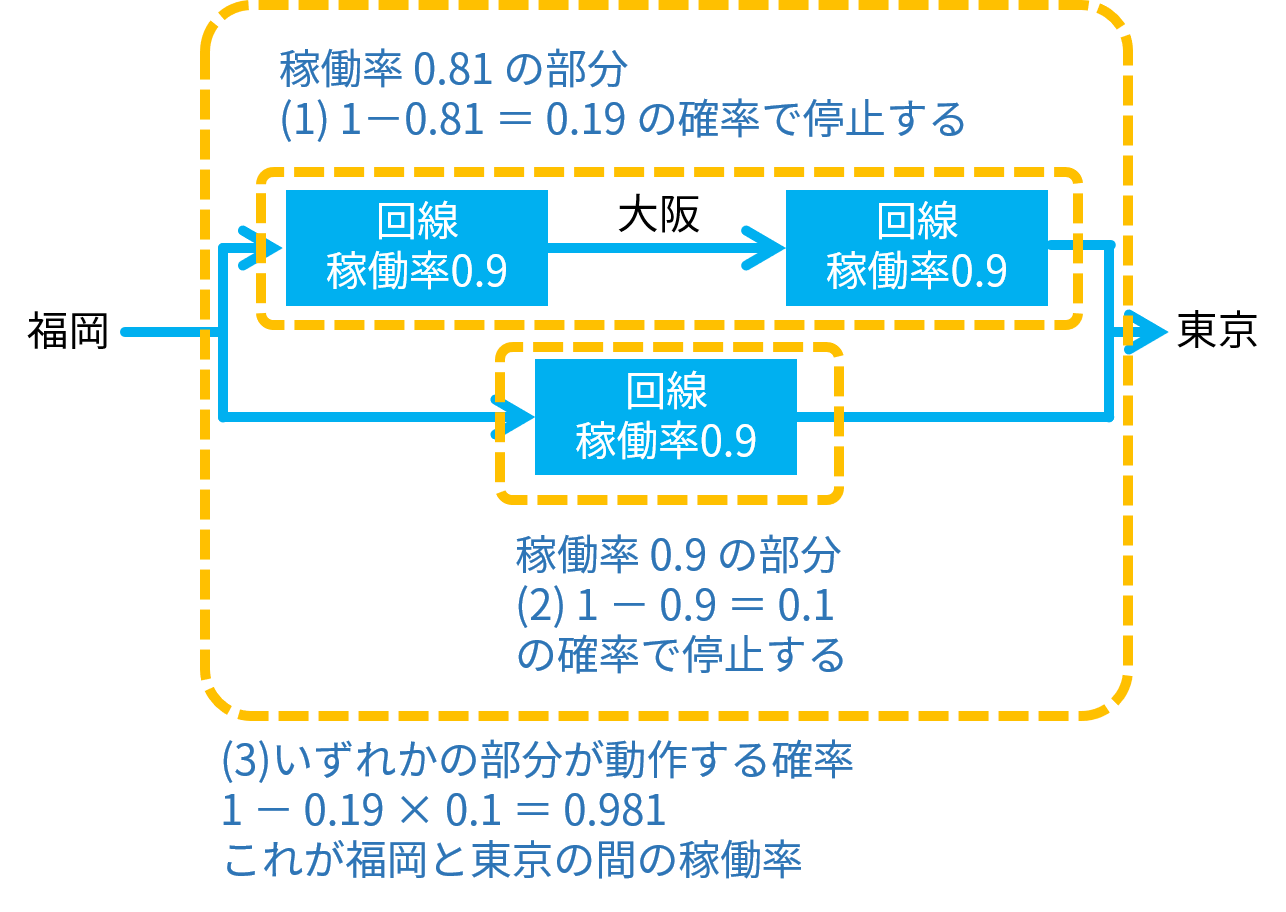
したがって、選択肢ウが正解です。
正解 ウ
MTBF と MTTR という言葉が登場する問題
最後は、MTBF と MTTRという言葉が登場する問題です。もう一度、言葉の意味を確認しておきましょう。
MTBF( Mean Time Between Failire )は「動作している時間」で、MTTR( Mean Time To Repair )は「停止している時間」です。
MTBF が 45 時間で MTTR が5時間の装置がある。この装置を二つ直列に接続したシステムの稼働率は幾らか。
ア 0.81 イ 0.90 ウ 0.95 エ 10.99
問題に示された MTBF と MTTR の値から装置の稼働率を求めると、以下のように 0.9 になります。
- 装置の稼働率
- = MTBF / (MTBF+MTTR)
- = 45 時間 / ( 45 時間 + 5 時間)
- = 0.9
稼働率 0.9 の装置を 2 つ直列に接続したシステムの稼働率は、もう図を描かなくても計算できると思いますが、
になります。したがって、選択肢アが正解です。
正解 ア
稼働率の計算方法と問題の解き方を、ご理解いただけましたでしょうか。
基本情報技術者試験の会場には、電卓を持ち込めないので、問題を練習するときには、電卓を使わずに手作業で計算してください。
はじめは時間がかかるかもしれませんが、何問か練習しているうちに、だんだん速く計算できるようになるはずです。
それでは、またお会いしましょう!
label 関連タグ
免除試験を受けた 74.9% の方が、科目A免除資格を得ています。
※独習ゼミは、受験ナビ運営のSEプラスによる試験対策eラーニングです。

一般常識で解ける マネジメント と ストラテジ の計算方法|かんたん計算問題
update
ITエンジニアも知っておくべき 財務会計 の計算方法|かんたん計算問題
update
略語でわかる MIPS の計算方法|かんたん計算問題
update
ビットパターンの計算問題|かんたん計算問題
update
構造と仕組みを知ればできる 磁気ディスク装置 の計算方法|かんたん計算問題
update
音声サンプリングの計算方法がわかる|かんたん計算問題
update
通信ネットワークの計算方法がわかる|かんたん計算問題
update
工数の計算方法がわかる|かんたん計算問題
update
稼働率の計算方法がわかる|かんたん計算問題
update
期待値の計算方法がわかる|かんたん計算問題
update
『プログラムはなぜ動くのか』(日経BP)が大ベストセラー
IT技術を楽しく・分かりやすく教える“自称ソフトウェア芸人”
大手電気メーカーでPCの製造、ソフトハウスでプログラマを経験。独立後、現在はアプリケーションの開発と販売に従事。その傍ら、書籍・雑誌の執筆、またセミナー講師として活躍。軽快な口調で、知識0ベースのITエンジニアや一般書店フェアなどの一般的なPCユーザの講習ではダントツの評価。
お客様の満足を何よりも大切にし、わかりやすい、のせるのが上手い自称ソフトウェア芸人。
主な著作物
- 「プログラムはなぜ動くのか」(日経BP)
- 「コンピュータはなぜ動くのか」(日経BP)
- 「出るとこだけ! 基本情報技術者」 (翔泳社)
- 「ベテランが丁寧に教えてくれる ハードウェアの知識と実務」(翔泳社)
- 「ifとelseの思考術」(ソフトバンククリエイティブ) など多数









