サーチのアルゴリズム (2) 二分探索法|新しい擬似言語で学ぶ 科目 B アルゴリズムとプログラミング入門

基本情報技術者試験は、 2023 年 4 月から新制度で実施されています。
この連載では、新制度で採用された新しい擬似言語(旧制度の擬似言語とは、表記方法に違いがあります)を使って、試験のシラバス(情報処理技術者試験における知識・技能の細目)に示されている代表的なアルゴリズムとデータ構造を、プログラミング入門者向けにやさしく解説します。 受験対策としてだけでなく、アルゴリズムとプログラミングの基礎知識を習得するために、ぜひお読みください。
今回は、効率的なサーチアルゴリズムである 二分探索法 を取り上げます。
二分探索法のアルゴリズム
図 1 に示したように、裏返された状態で 7 枚のトランプが並んでいるとします。 これらの中から、マークは何でもよいので 5 のカードを見つけるとしたら、どうしますか? 「先頭(左端が先頭だとします)から順に 1 枚ずつめくって 5 かどうかをチェックする」と考えたなら、それで正解です。 そのアルゴリズムは、第 4 回の記事で紹介した「線形探索法」です。
それでは、これら 7 枚のトランプが昇順(小さい順)にソートされているとしたら、どうしますか? 線形探索法より効率的なアルゴリズムがありますので、ちょっと考えてみてください。 ポイントは、最初にどこをめくるかです。

勘のいい人は「真ん中のカードをめくって、その値から探索対象を前側か後ろ側に絞り込む」というアルゴリズムを思い付いたでしょう。 それで正解です。 そのアルゴリズムを「二分探索法」と呼びます。
トランプ(プログラムでは配列)がランダムに並んでいたら、線形探索法を使うことになりますが、ソートされているなら二分探索法を使った方が効率的です。 7 枚のトランプがある場合には、線形探索法では最大で 7 回カードをめくりますが、二分探索法では最大で 3 回カードをめくるだけで済みます。
図 2 に二分探索法で目的の値が見つかるまでの手順の例を示します。
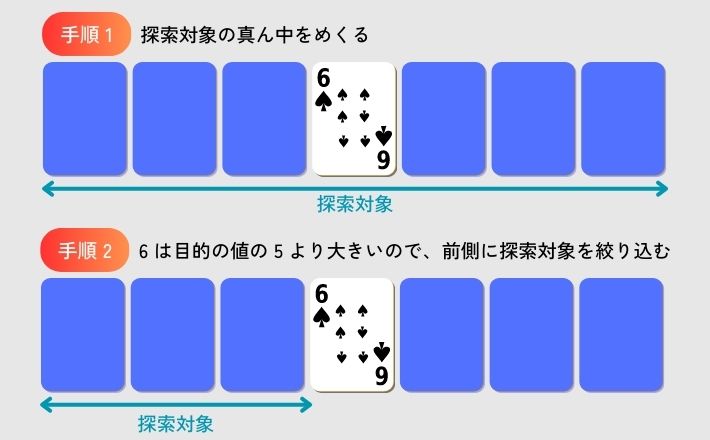
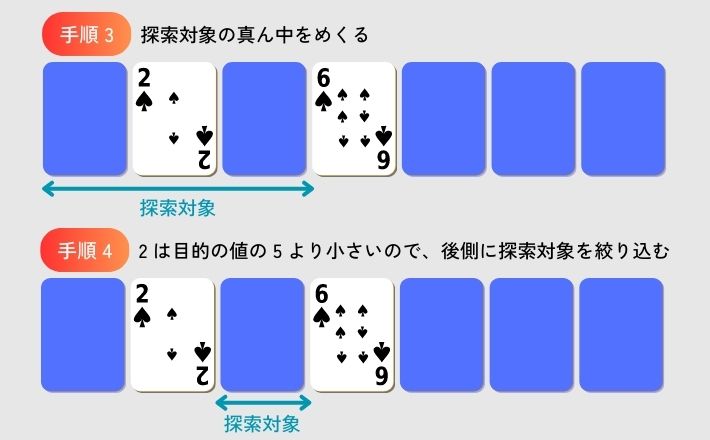
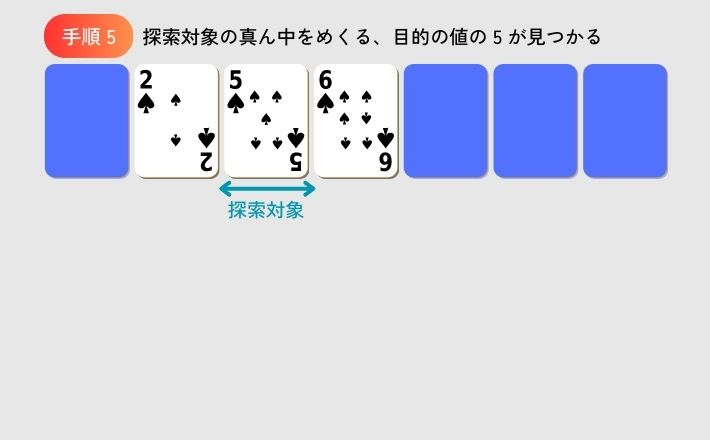
7 枚のカードの探索対象は、 7 枚 → 3 枚 → 1 枚 と二分割されていきます。 だから二分探索と呼ぶのです。
ここでは、最後の 1 枚で見つかっていますが、その前の段階で見つかることも、最後までチェックして見つからないこともあります。
二分探索法のプログラムの例
リスト 1 は、二分探索法のプログラムの例です。 要素数 7 個の整数型の配列 a (昇順にソートされていて、要素番号は 0 から始まるとします)の中から変数 x と同じ値を見つけます。
二分探索法のプログラムには、決まりきった書き方があります。 これを、空手の型のように、プログラムの型として覚えてください。
なお、第 4 回の記事で説明したサーチアルゴリズムの基本である
「見つかった場合は、その時点で探索を終了する」
「見つからなかった場合は、配列の要素番号としてあり得ない -1 を探索の結果とする」
format_quote
は、二分探索法でも同様です。 繰り返しを中断するのに、 break 文を使うことも使わないこともできるのも、線形探索法と同様です。 リスト 1 では、 break 文を使っていません。
整数型の配列 a ← { 1, 2, 5, 6, 8, 10, 12 } 整数型 x, pos, left, mid, right // 変数に初期値を設定する x ← 5 // 見つける値 pos ← -1 // 探索の結果 left ← 0 // 探索対象の左端の要素番号 right ← 6 // 探索対象の右端の要素番号 // まだ探索対象があり、かつ、まだ見つかってない限り、探索を繰り返す while (left ≦ right and pos = -1) mid ← (left + right) ÷ 2 // 真ん中の要素の要素番号を得る if (a[mid] = x) // 真ん中の要素が見つける値と同じ場合 pos ← mid // 探索の結果に見つかった位置を設定する elseif (a[mid] > x) // 真ん中の要素が見つける値より大きい場合 right ← mid - 1 // 真ん中より前側に探索対象を絞り込む else // 真ん中の要素が見つける値より小さい場合 left ← mid + 1 // 真ん中より後側に探索対象を絞り込む endif endwhile // 探索の結果を表示する print(pos)
リスト 1 の内容を詳しく説明しましょう。
配列 a から変数 x と同じ値を見つけます。 探索の結果は、変数 pos に格納します。 ここでは、変数 x に 5 を設定しています。 変数 pos は、見つからなかったことを意味する -1 で初期化しています。
探索によって、 5 は a[2] に見つかるので、変数 pos の値は 2 で上書きされます。 最後にある print は、引数の値を画面に表示する手続だとします。 print(pos) によって、探索の結果が画面に表示されます。ここまでは、第 4 回で紹介した線形探索のプログラムと同様です。
二分探索法の型
変数 left 、 mid 、 right は、探索対象の左端、真ん中、左端の要素番号です。 これら 3 つの変数を使うことが、二分探索法の型です。 最初は、配列全体が探索対象なので、変数 left に先頭の要素番号の 0 を設定し、変数 right に末尾の要素番号の 6 を設定します。
二分探索法では、 while 文を使った繰り返しを行います。 while 文のカッコの中に記述する
left ≦ right and pos = -1
という条件も、二分探索法の型です。 これは、「まだ探索対象があり、かつ、まだ見つかってない」という条件を意味しています。
pos = -1 が「まだ見つかっていない」という条件であることはわかると思いますが、どうして left ≦ right が「まだ探索対象がある」という条件になるか、わかりますか?
leftの初期値は配列の先頭であり、 right の初期値は配列の末尾なので
left < right
です。 while文の繰り返しで、徐々に探索対象を狭めていくと、最後の 1 個の要素をチェックするときに
left = right
になります。 したがって、 left < right から left = right までは探索対象があるので、これらをまとめて記述して
left ≦ right
になるのです。
while 文で繰り返される処理の内容も、二分探索法の型です。
まず
mid ← (left + right) ÷ 2
で、現在の探索対象の真ん中の要素番号を変数 mid に得ています。 真ん中は (left + right) ÷ 2 という計算で得られます。 変数 left とright は、整数型なので、割り算の小数点以下はカットされます。
次に、 if 文で真ん中の a[mid] と変数 x の値を比べて、処理を 3 つに分岐させます。
- looks_one もしも、真ん中の要素が見つける値と同じ場合
a[mid] = x - arrow_forward 探索の結果に見つかった位置を設定します
pos ← mid - looks_two そうではなく、もしも、真ん中の要素が見つける値より大きい場合
a[mid] > x - arrow_forward 真ん中より前側に探索対象を絞り込みます
right ← mid - 1 - looks_3 そうではない場合
else - arrow_forward 真ん中の要素が見つける値より小さい場合なので、真ん中より後側に探索対象を絞り込みます
left ← mid + 1
二分探索法の穴埋め問題にチャレンジする
試験対策として、二分探索法の穴埋め問題にチャレンジしてみましょう。
整数型の配列 a ← { 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 13 } 整数型 x, pos, left, mid, right x ← 8 pos ← -1 left ← 0 right ← a while (b) mid ← (left + right) ÷ 2 if (a[mid] = x) pos ← mid elseif (a[mid] > x) right ← mid - 1 else left ← mid + 1 endif endwhile print(pos)
解答群
| a | b | |
|---|---|---|
| ア | 9 | left ≦ right and pos = -1 |
| イ | 9 | right ≦ left and pos = -1 |
| ウ | 10 | left ≦ right and pos = -1 |
| エ | 10 | right ≦ left and pos = -1 |
空欄 a は、探索対象の右端の要素番号に、配列の末尾の要素番号を設定する処理です。 ここでは、配列の要素数が 10 個で、要素番号は 0 から始まるので、末尾の要素番号は 9 です。
空欄 b は、探索を繰り返す条件です。 ここには、「まだ探索対象があり、かつ、まだ見つかってない」を意味する
left ≦ right and pos = -1
を指定します。 したがって、選択肢アが正解です。
今回は、効率的なサーチアルゴリズムである二分探索法を取り上げました。
次回は、再帰のアルゴリズムを取り上げる予定です。
それでは、またお会いしましょう!
label 関連タグ免除試験を受けた 74.9% の方が、科目A免除資格を得ています。
※独習ゼミは、受験ナビ運営のSEプラスによる試験対策eラーニングです。

マージソート|新しい擬似言語で学ぶ 科目 B アルゴリズムとプログラミング入門
update
二分木の深さ優先探索と幅優先探索|新しい擬似言語で学ぶ 科目 B アルゴリズムとプログラミング入門
update
比べてわかるキューとスタックの仕組み|新しい擬似言語で学ぶ 科目 B アルゴリズムとプログラミング入門
update
「リスト」というデータ構造|新しい擬似言語で学ぶ 科目 B アルゴリズムとプログラミング入門
update
サーチのアルゴリズム (3) ハッシュ表探索法のアルゴリズム|新しい擬似言語で学ぶ 科目 B アルゴリズムとプログラミング入門
update
クイックソートのアルゴリズム|新しい擬似言語で学ぶ 科目 B アルゴリズムとプログラミング入門
update
再帰呼び出しのアルゴリズム|新しい擬似言語で学ぶ 科目 B アルゴリズムとプログラミング入門
update
サーチのアルゴリズム (2) 二分探索法|新しい擬似言語で学ぶ 科目 B アルゴリズムとプログラミング入門
update
サーチのアルゴリズム (1) 線形探索法|新しい擬似言語で学ぶ 科目 B アルゴリズムとプログラミング入門
update
多重ループを使うバブルソート|新しい擬似言語で学ぶ 科目 B アルゴリズムとプログラミング入門
update
『プログラムはなぜ動くのか』(日経BP)が大ベストセラー
IT技術を楽しく・分かりやすく教える“自称ソフトウェア芸人”
大手電気メーカーでPCの製造、ソフトハウスでプログラマを経験。独立後、現在はアプリケーションの開発と販売に従事。その傍ら、書籍・雑誌の執筆、またセミナー講師として活躍。軽快な口調で、知識0ベースのITエンジニアや一般書店フェアなどの一般的なPCユーザの講習ではダントツの評価。
お客様の満足を何よりも大切にし、わかりやすい、のせるのが上手い自称ソフトウェア芸人。
主な著作物
- 「プログラムはなぜ動くのか」(日経BP)
- 「コンピュータはなぜ動くのか」(日経BP)
- 「出るとこだけ! 基本情報技術者」 (翔泳社)
- 「ベテランが丁寧に教えてくれる ハードウェアの知識と実務」(翔泳社)
- 「ifとelseの思考術」(ソフトバンククリエイティブ) など多数











