プログラムを分割するコツがわかる練習問題|アルゴリズムとプログラミング問題を解くコツ

科目 B 問題の新しい擬似言語に合わせて、プログラムを変更しました。
なお、本記事では過去問題を一部改変しています。
この連載では、基本情報技術者試験で、多くの受験者が苦手意識を持っている科目 B 試験 アルゴリズムとプログラミング分野の「アルゴリズム穴埋め問題」に的を絞って、正解を見出すポイントを詳しく説明します。
苦手を克服するには、短いプログラムを何度も練習して、穴埋めに慣れることが重要です。
そのために、実際の試験問題の一部をアレンジした練習問題を作りました。 とても短い問題ですので、気軽に取り組んでください。
もくじ
練習問題
手続 TabSpc は、タブ文字を展開するプログラムである。
- TabSpc は、引数で指定された文字型配列 Src[] を先頭から調べ、 Src[] 中のすべてのタブ文字をそれぞれ一つ以上の間隔文字(スペース)に変換して、引数で指定された文字型配列 Dst[] に格納する。
- 文字型配列の各要素には、文字を 1 文字ずつ順に格納し、最後の文字の次の要素にはシステム定数である EOS を格納する。 なお、配列の添字は 1 から始まり、添字の値を文字位置と呼ぶ。
- Src[] 中にタブ文字が出現した場合、次の文字が最も近い右のタブ位置に格納されるように、タブ文字を一つ以上の間隔文字に置換して、 Dst[] (要素数は十分に大きいとする)に格納する。 ここで、タブ位置とは、整数型の引数 TabGap で渡されるタブ間隔(≧ 2)を用いて、次の式で計算される文字位置である。
タブ位置 = タブ間隔 × n + 1 ( n は 1 以上の整数)
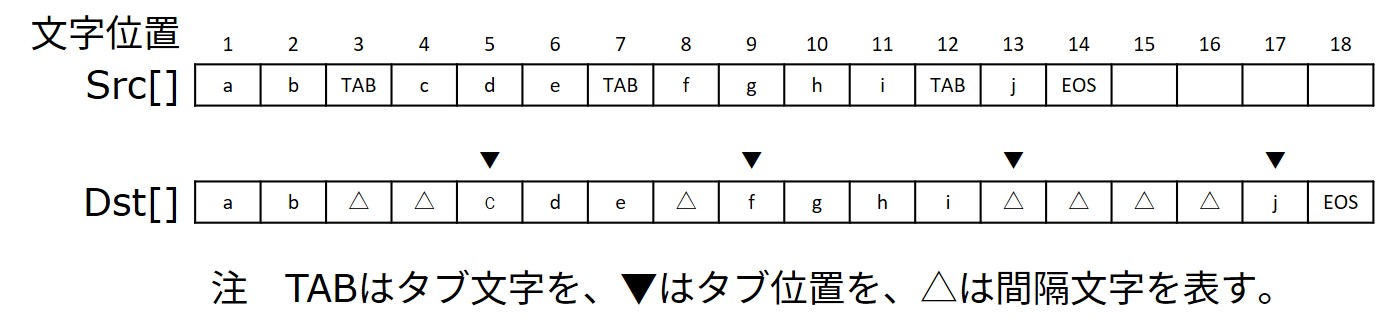
- タブ間隔が 4 のときの実行例を図に示す。 “j” を Dst[] のタブ位置である文字位置 13 ( = 4 × 3 + 1 )に格納したのでは、タブ文字が間隔文字に置き換わらないので、最も近い右のタブ位置である文字位置 17 ( = 4 × 4 + 1 )に格納する。
[プログラム]
◯TabSpc(文字型の配列: Src, 文字型の配列: Dst, 整数型: TabGap)
整数型: Sidx, Didx, N, TabPos
Sidx ← 1
Didx ← 1
while (Src[Sidx] が EOS とは等しくない) /* EOS: 文字列の終わりを表すシステム定数 */
if (Src[Sidx] が TAB と等しい) /* TAB: タブ文字を表すシステム定数 */
N ← ( a ) ÷ TabGap
TabPos ← TabGap × N + 1
while (Didx が TabPos より小さい)
Dst[Didx] ← SPC /* SPC: 間隔文字を表すシステム定数 */
b
endwhile
else
c
Didx ← Didx + 1
endif
Sidx ← Sidx + 1
endwhile
Dst[Didx] ← EOS
設問
プログラム中のに入れる正しい答えを、解答群の中から選べ。
a に関する解答群
- ア
- Didx + 1
- イ
- Didx – 1
- ウ
- Didx + TabGap + 1
- エ
- Didx + TabGap – 1
b 、 c に関する解答群
- ア
- Didx ← Didx + 1
- イ
- Dst[Didx] ← Src[Sidx]
- ウ
- Dst[Didx + 1] ← Src[Sidx]
- エ
- Dst[Didx] ← Src[Sidx + 1]
ポイント1: プログラムを区切って見る
私の講師経験上、「アルゴリズムが苦手です!」という受講者の多くは、プログラム全体を一気に見て理解しようとします。 それでは、なかなか理解できなくて当然です。
プログラムというものは、全体をいくつかの部分に区切って見るものだからです。 「そんなこと言われても、どうやって区切ったらよいかわかりません!」だと思いますので、区切り方をアドバイスしましょう。
プログラムの処理の流れの種類は、
順次(まっすぐ進む)
分岐(条件に応じて選択する)
反復(条件に応じて繰り返す)
の 3 つです。
擬似言語では、何も指定しなければ順次になり、 if と endif で囲めば分岐になり、 while と endwhile で囲めば反復になります。 これらの表記に注目すれば、機械的に区切れるはずです。
プログラムを区切った例を下図に示します。
◯TabSpc(文字型の配列: Src, 文字型の配列: Dst, 整数型: TabGap)順次 整数型: Sidx, Didx, N, TabPos Sidx ← 1 Didx ← 1while (Src[Sidx] が EOS とは等しくない) /* EOS: 文字列の終わりを表すシステム定数 */反復 endwhileDst[Didx] ← EOS順次 if (Src[Sidx] が TAB と等しい) /* TAB: タブ文字を表すシステム定数 */分岐 N ← ( a ) ÷ TabGap TabPos ← TabGap × N + 1 while (Didx が TabPos より小さい) Dst[Didx] ← SPC /* SPC: 間隔文字を表すシステム定数 */ b endwhile else c Didx ← Didx + 1 endif Sidx ← Sidx + 1
プログラムを区切ったことで、空欄 a 、空欄 b 、空欄 c があるのが、分岐の部分だとわかります。 それがわかったら(ここが大事です!)、プログラム全体ではなく、分岐の部分だけを見てください。
この分岐は、どのような条件で分岐するのでしょう。
Src[Sidx] が TAB と等しい
という条件が真なら空欄 a と空欄 b がある上側の処理を行い、そうでないなら空欄 c がある下側の処理を行います。 これもプログラムの区切りです。 これらの区切りごとに、プログラムを見てください。
ポイント2: わかりやすい部分を先に穴埋めする
空欄の穴埋めは、わかりやすい部分から先に行ってください。 分岐の下側にある空欄 c の穴埋めが、わかりやすいでしょう。
ここでは、 Src[Sidx] が TAB と等しい という条件が真でないときの処理なのですから、 Src[] から取り出した文字(タブ文字でない文字)を、そのまま Dst[] に格納する処理です。
したがって、
Dst[Didx] ← Src[Sidx]
が適切であり、選択肢イが正解です。
ポイント3: 選択肢をヒントにして考える
それでは、空欄 a と空欄 b がある分岐の上側の処理を見てみましょう。
ここは、 Src[Sidx] が TAB と等しい という条件が真のときの処理なので、タブ文字を間隔文字に置き換える処理です。
N ← ( a ) ÷ TabGap TabPos ← TabGap × N + 1 while (Didx が TabPos より小さい) Dst[Didx] ← SPC /* SPC: 間隔文字を表すシステム定数 */ b endwhile
空欄 a より空欄 b の方がわかりやすそうなので、空欄 b の穴埋めを先に行うことにしましょう。
さて、どのような処理をすればよいのでしょうか?
こういうことは、腕を組んで考えることではありません。 基本情報技術者試験の問題は、すべて多岐選択式です。 したがって、解答群に示された選択肢をヒントにして考えてください。
空欄 b の選択肢を以下に示します。
b 、 c に関する解答群
- ア
- Didx ← Didx + 1
- イ
- Dst[Didx] ← Src[Sidx]
- ウ
- Dst[Didx + 1] ← Src[Sidx]
- エ
- Dst[Didx] ← Src[Sidx + 1]
空欄 b の処理が、
選択肢アだったら?
選択肢イだったら?
選択肢ウだったら?
選択肢エだったら?
と考えると「あっ、そうか!」と気付くでしょう。
空欄 b は、 Dst[Didx] に必要な数だけ SPC (間隔文字)を格納する処理です。 1 つ SPC を格納したら、 Didx に 1 を加えて格納先を 1 つ先に進めます。
したがって、選択肢アの
Didx ← Didx + 1
が正解です。
ポイント4: 具体例を想定し、想定した値で計算する
それでは、最後に残った空欄 a の穴埋めです。
ここは、空欄 a から N( タブ位置の計算式の n )の値を求め、さらに N から TabPos (タブ位置)の値を求める処理です。 これは、かなり難しそうです。
N ← ( a ) ÷ TabGap
TabPos ← TabGap × N + 1
こういうときに頼りになるのが、問題に示された具体例です。
問題には、 TabGap(タブ間隔)= 4 としたときの具体例の図が示されていて、そこには、問題に示された
タブ位置 = タブ間隔 × n + 1 ( n は 1 以上の整数)
という計算で得られるタブ位置も示されています。 そして、
“j” を Dst[] のタブ位置である文字位置 13 ( = 4 × 3 + 1 )に格納したのでは、タブ文字が間隔文字に置き換わらないので、最も近い右のタブ位置である文字位置 17 ( = 4 × 4 + 1 )に格納する
という注意書きがあります。 おそらく、この注意書きが答えを見出すポイントなのでしょう。
この注意書きに注目して、具体例を想定してみましょう。
Src[] の文字位置 12 にあるタブ文字を展開するときに、 Dst[] のタブ位置が 13 でなく 17 になればよいわけです。
空欄 a の選択肢を見ると、どれも Dst[] の格納先である Didx が含まれています。 想定した場面では、
Didx = 13
TabGap = 4
なので、選択肢ア~エの値は、以下になります。
整数の割り算では、小数点以下がカットされることに注意してください。
-
a に関する解答群
- ア
- Didx + 1 = 12 + 1 = 13
- イ
- Didx = 1 = 12 = 1 = 11
- ウ
- Didx + TabGap + 1 = 12 + 4 + 1 = 17
- エ
- Didx + TabGap = 1 = 12 + 4 = 1 = 15
この 13, 11, 17, 15 をプログラムの空欄 a に入れて、 TabPos を求めると以下になります。
選択肢ア N ← (13) ÷ 4 ・・・ N は 3 になる。 TabPos ← 4 × N + 1 ・・・ TabPos は 13 になる。 選択肢イ N ← (11) ÷ 4 ・・・ N は 2 になる。 TabPos ← 4 × N + 1 ・・・ TabPos は 9 になる。 選択肢ウ N ← (17) ÷ 4 ・・・ N は 4 になる。 TabPos ← 4 × N + 1 ・・・ TabPos は 17 になる。 選択肢エ N ← (15) ÷ 4 ・・・ N は 3 になる。 TabPos ← 4 × N + 1 ・・・ TabPos は 13 になる。
ここでは、 TabPos が 17 になればよいので、選択肢ウが正解です。 やはり、注意書きが答えを見出すポイントでした。
解答a - ウ, b - ア, c - イ
「習うより慣れろ」ということわざがあります。 アルゴリズム穴埋め問題の克服に関しては、正にその通りでしょう。
この連載では、これからも短い練習問題を掲載していきますので、穴埋めに慣れることを目指してください。
正解を見出すポイントとして、同じことが示されることもあると思いますが、それは、多くの問題に共通したポイントがあるからです。
それでは、またお会いしましょう!
label 関連タグ免除試験を受けた 74.9% の方が、科目A免除資格を得ています。
※独習ゼミは、受験ナビ運営のSEプラスによる試験対策eラーニングです。

具体的な値を入れるとプログラムがわかる練習問題|アルゴリズムとプログラミング問題を解くコツ
update
具体例からヒントを掴む練習問題|アルゴリズムとプログラミング問題を解くコツ
update
プログラムを分割するコツがわかる練習問題|アルゴリズムとプログラミング問題を解くコツ
update
手順をヒントにトレースする練習問題|アルゴリズムとプログラミング問題を解くコツ
update
トレースのテクニックが身につく練習問題|アルゴリズムとプログラミング問題を解くコツ
update
2進数を掛け算するプログラム | アルゴリズムとプログラミング問題を解くコツ
update
ヒープを配列で実現するプログラム|アルゴリズムとプログラミング問題を解くコツ
update
ルールに従って検査文字(チェックディジット)を求めるプログラム|アルゴリズムとプログラミング問題を解くコツ
update
配列のマッチング(突合せ)を行うプログラム|アルゴリズムとプログラミング問題を解くコツ
update
2進数の知識が必要なプログラム|アルゴリズムとプログラミング問題を解くコツ
update
『プログラムはなぜ動くのか』(日経BP)が大ベストセラー
IT技術を楽しく・分かりやすく教える“自称ソフトウェア芸人”
大手電気メーカーでPCの製造、ソフトハウスでプログラマを経験。独立後、現在はアプリケーションの開発と販売に従事。その傍ら、書籍・雑誌の執筆、またセミナー講師として活躍。軽快な口調で、知識0ベースのITエンジニアや一般書店フェアなどの一般的なPCユーザの講習ではダントツの評価。
お客様の満足を何よりも大切にし、わかりやすい、のせるのが上手い自称ソフトウェア芸人。
主な著作物
- 「プログラムはなぜ動くのか」(日経BP)
- 「コンピュータはなぜ動くのか」(日経BP)
- 「出るとこだけ! 基本情報技術者」 (翔泳社)
- 「ベテランが丁寧に教えてくれる ハードウェアの知識と実務」(翔泳社)
- 「ifとelseの思考術」(ソフトバンククリエイティブ) など多数










