具体的な値を入れるとプログラムがわかる練習問題|アルゴリズムとプログラミング問題を解くコツ

科目 B 問題の新しい擬似言語に合わせて、プログラムを変更しました。
なお、本記事では過去問題を一部改変しています。
この連載では、基本情報技術者試験で、多くの受験者が苦手意識を持っている科目 B 試験 アルゴリズムとプログラミング分野の「アルゴリズム穴埋め問題」に的を絞って、正解を見出すポイントを詳しく説明します。
苦手を克服するには、短いプログラムを何度も練習して、穴埋めに慣れることが重要です。
そのために、実際の試験問題の一部をアレンジした練習問題を作りました。とても短い問題ですので、気軽に取り組んでください。
練習問題
RadixConv 関数は、 M 進数字列( 2 ≦ M ≦ 16 )を、 N 進数字列( 2 ≦ N ≦ 16 )に基数変換するプログラムである。
- M 進数字列および N 進数字列は、数字を表す文字だけで構成され、空白文字は含まない。 11 ~ 16 進数の 10 以上の数字には、 “A” ~ “F” のアルファベットを用いる。
- RadixConv 関数は、 M 進数字列を整数値に変換した後、その整数値を N 進数字列に変換する。その際に、 M 進数字列を整数値に変換する MToInt 関数と、整数値を N 進数字列に変換する IntToN 関数を使う。
- MToInt 関数と IntToN 関数は、数字を整数に変換して返す ToInt 関数、整数値を数字に変換する ToStr 関数、文字列の長さを返す Length 関数、および文字列の一部を切り出して返す SubStr 関数を使う。
- このプログラムで使われる関数の引数と戻り値の仕様を表 1 ~ 7 に示す。
| 引数/戻り値 | データ型 | 意味 |
|---|---|---|
| Frdx | 整数型 | 変換元の数字列の基数( 2 ≦ Frdx ≦ 16 ) |
| Fnum | 文字列 | 変換元の数字列 |
| Trdx | 整数型 | 変換後の数字列の基数( 2 ≦ Trdx ≦ 16 ) |
| 戻り値 | 文字列型 | 変換後の数字列 |
| 引数/戻り値 | データ型 | 意味 |
|---|---|---|
| Rdx | 整数型 | 変換元の数字列の基数( 2 ≦ Rdx ≦ 16 ) |
| Num | 文字列型 | 変換元の数字列 |
| 戻り値 | 整数型 | 変換後の整数 |
| 引数/戻り値 | データ型 | 意味 |
|---|---|---|
| Val | 整数型 | 変換元の整数 |
| Rdx | 整数型 | 変換後の数字列の基数( 2 ≦ Rdx ≦ 16 ) |
| 戻り値 | 文字列型 | 変換後の数字列 |
| 引数/戻り値 | データ型 | 意味 |
|---|---|---|
| P | 文字型 | 変換元の数字( “0”, “1”, …, “F” ) |
| 戻り値 | 整数型 | 変換後の整数 |
| 引数/戻り値 | データ型 | 意味 |
|---|---|---|
| Q | 整数型 | 変換元の整数( 0 ≦ Q ≦ 15 ) |
| 戻り値 | 文字型 | 変換後の数字 |
| 引数/戻り値 | データ型 | 意味 |
|---|---|---|
| S | 文字列型 | 長さを求める文字列 |
| 戻り値 | 整数型 | 文字列の長さ |
| 引数/戻り値 | データ型 | 意味 |
|---|---|---|
| S | 文字列型 | 切り出し元の文字列 |
| Idx | 整数型 | 切り出しを始める位置(先頭を 1 とする) |
| N | 整数型 | 切り出す文字数 |
| 戻り値 | 文字列型 | S の先頭から Idx の位置から N 文字を返す |
[プログラム]
◯文字列型: RadixConv(整数型: Frdx, 文字列型: Fnum, 整数型: Trdx)
return IntToN(MToInt(Frdx, Fnum), Trdx)
◯整数型: MToInt(整数型: Rdx, 文字列型: Num)
整数型: Idx, Val
Val ← 0
for (Idx を 1 から Length(Num) 以下まで 1 つずつ増加)
Val ← a + ToInt(Substr(Num, Idx, 1))
endfor
return Val
◯文字列型: IntToN(整数型: Val, 整数型: Rdx)
整数型: Quo /* 商 */
整数型: Rem /* 剰余 */
文字列型: Num
b
Num ← ""
while (Quo が Rdx 以上)
Rem ← Quo mod Rdx
Num ← ToStr(Rem) + Num /* + は文字列を連結する演算子 */
c
endwhile
d
return Num
add_alert注 ToInt 関数、ToStr 関数、Length 関数、SubStr 関数のプログラムは示さないが、正しく作成されているとする。
設問 プログラム中のに入れる正しい答えを、解答群の中から選べ。
a に関する解答群
ア Rdx
イ Val
ウ Val × Rdx
エ Val ÷ Rdx
b ~ d に関する解答群
- ア
- Quo ← Quo ÷ Rdx
- イ
- Quo ← Quo ÷ Rem
- ウ
- Quo ← Rdx
- エ
- Quo ← Rem ÷ Rdx
- オ
- Quo ← Val
- カ
- Rem ← Rdx
- キ
- Rem ← Val
- ク
- Num ← ToStr(Quo) + Num
- ケ
- Num ← ToStr(Rem) + Num
ポイント1: 自分にわかりやすい具体例を想定する
RadixConv 関数は、 M 進数字列を N 進数字列に基数変換するプログラムですが、 M と N のままではプログラムを読むことはできません。
M と N に、自分に分かりやすい具体例を想定してください。
ここでは以下のように想定します。
- M = 10, N = 2 として、 10 進数字列を 2 進数字列に変換すること
- 具体的な数字列として、 “12” という 10 進数字列を “1100” という 2 進数字列に変換する
これらの想定によって、 RadixConv 関数は、以下の処理を行うことになります。
図 RadixConv 関数が行う処理の具体例
◯文字列型: RadixConv(整数型: Frdx, 文字列型: Fnum, 整数型: Trdx) return IntToN(MToInt(Frdx, Fnum), Trdx) 10"12"2戻り値 "1100"10"12"2
これで、プログラムの内容を読めるはずです。同じ具体例を想定して、他の関数のプログラムも読んでみましょう。
ポイント2: 具体例で処理内容を理解し、選択肢をヒントにして穴埋めをする
まず、空欄 a がある MToInt 関数です。 MToInt 関数は、数字列を数値に変換して返します。
想定した具体例で、プログラムを読んでみましょう。
ここでは、
Rdx = 10 進数の数字列 Num = “12” を、
Val = 12 という整数値に変換
して返すことを想定します。
図 MToInt 関数が行う処理の具体例
◯MToInt(整数型: Rdx, 文字列型: Num) 整数型: Idx, Val Val ← 0 for (Idx を 1 から Length(Num) 以下まで 1 つずつ増加) Val ← a + ToInt(Substr(Num, Idx, 1)) endfor return Val 10"12"2"12" の先頭から 1 文字ずつ取り出し、それを整数に変換する変換後の 12 を返す
この想定では、 Length(Num) は 2 です。したがって、 Idx をループカウンタとした繰り返しは、 Idx を 1, 2 と変化させて繰り返します。
繰り返しの中にある
Substr(Num, Idx, 1)
は、 “12” の先頭から 1 文字ずつ “1”, “2” を取り出します。
そして、
ToInt(Substr(Num, Idx, 1))
は、 “1”, “2” という数字を、 1, 2 という数値に変換します。関数は、 12 という戻り値を返すので、空欄 a がある
Val ← a+ ToInt(Substr(Num, Idx, 1))
は、 1, 2 から 12 を作り出し、それを Val に格納する処理です。
それでは、どうすれば 1, 2 から 12 を作り出せるでしょう。
もしも、手順が思い浮かばないなら、選択肢を見てください。選択肢の中に必ず正解があるのですから、選択肢を見れば「あっ、これだ!」と気付くはずです。
a に関する解答群
ア Rdx
イ Val
ウ Val × Rdx
エ Val ÷ Rdx
1, 2 から 12 を作り出すには、 1 を 10 倍して、それに 2 を足せばよいのです。つまり、
Val ← a+ ToInt(Substr(Num, Idx, 1))
の部分が、
Val ← [Val × 10] + 2
になればよいのです。ここでは、 Rdx = 10 を想定しているので、これに該当するのは、 Val × Rdx (選択肢ウ)です。
ポイント3: 具体的な場面を想定して穴埋めを行う
今度は、空欄 b, 空欄 c, 空欄 d がある IntToN 関数です。 IntToN 関数は、整数値を数字列に変換して返します。
想定した具体例で、プログラムを読んでみましょう。ここでは、
Val = 12 という整数値を、
Rdx = 2 進数の数字列 Num = “1100” に変換
して返すことを想定します。
◯文字列型: IntToN(整数型: Val, 整数型: Rdx) 整数型: Quo /* 商 */ 整数型: Rem /* 剰余 */ 文字列型: Num b Num ← "" while (Quo が Rdx 以上) Rem ← Quo mod Rdx Num ← ToStr(Rem) + Num /* + は文字列を連結する演算子 */ c endwhile d return Num 122除算の余りを上位桁に連結する"1100"
Rem ← Quo mod Rdx
の部分で、 Quo を Rdx = 2 で除算した余りを Rem に格納し、
Num ← ToStr(Rem) + Num
の部分で、それを数字にして、戻り値 Num (数字列)上位桁に連結しています。
どうして、これらの処理で、 12 を “1100” に変換できるのでしょう。
これは、手作業で 10 進数を 2 進数に変換する手順に当てはめればわかるはずです。
手作業で 12 という 10 進数を 2 進数に変換するには、以下のように 12 を 2 で除算して余りを得る処理を繰り返します。
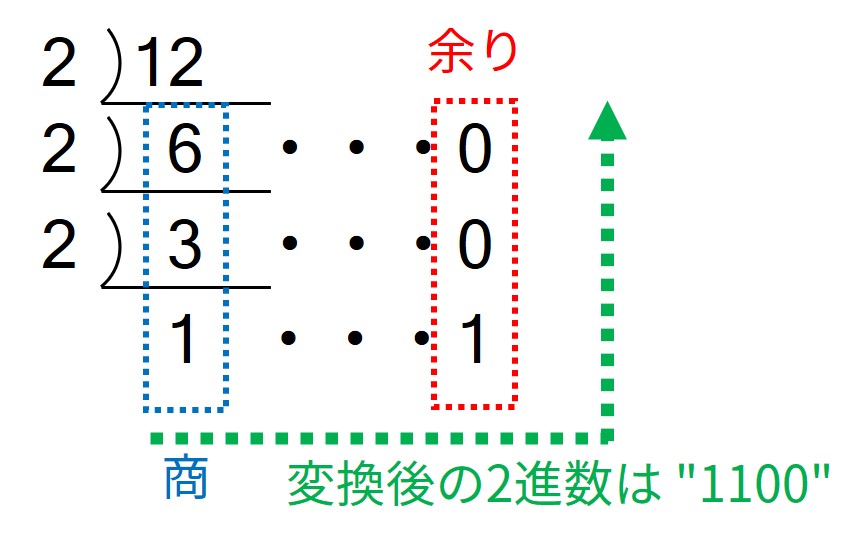
これによって、変換後の 2 進数が下位桁から順に得られるので、後から得られた値を文字に変換して上位桁に連結すればよいのです。
このプログラムでは、被除数が Quo で、序数が Rdx = 2 です。 Quo の初期値は、 Val = 12 であるべきなので、空欄 b は Quo ← Val (選択肢オ)です。
◯文字列型: IntToN(整数型: Val, 整数型: Rdx) 整数型: Quo /* 商 */ 整数型: Rem /* 剰余 */ 文字列型: Num b Num ← "" 122
Rem ← Quo mod Rdx の部分で、 Rem に除算の余りを求めたら、次の繰り返し処理に備えて、 Quo の値を除算の商で更新するべきなので、空欄 c は Quo ← Quo ÷ Rdx (選択肢ア)です。
while (Quo が Rdx 以上)
Rem ← Quo mod Rdx
Num ← ToStr(Rem) + Num /* + は文字列を連結する演算子 */
c
endwhile
除算の余りを上位桁に連結する
“Quo が Rdx 以上” つまり “Quo が 2 以上” という条件で繰り返しを行っているので、繰り返しを抜けると Quo は 1 になっています。繰り返しを抜けたら最後に、この 1 を文字に変換して上位桁に連結する必要があるので、空欄 d は Num ← ToStr(Quo) + Num (選択肢ク)です。
while (Quo が Rdx 以上)
Rem ← Quo mod Rdx
Num ← ToStr(Rem) + Num /* + は文字列を連結する演算子 */
Quo ← Quo ÷ Rdx
endwhile
d
return Num
"1100"
10 進数を 2 進数に変換する手順は、基本情報技術者試験の受験者なら必ず知っておくべきことです。
それを知っていたからこそ、 “12” という 10 進数字列を “1100” という 2 進数字列に変換することを想定して、問題を解けたのです。
もしも、試験の出題範囲の中に、まだ手を付けてない分野があるなら、それがアルゴリズム問題のテーマとなることもあるので、必ず学習しておきましょう。
解答a - ウ, b - オ, c - ア, d ― ク
「習うより慣れろ」ということわざがあります。アルゴリズム穴埋め問題の克服に関しては、正にその通りでしょう。
この連載は、今回で最終回になります。もしも、これまでの記事の中に理解が不十分なものがあれば、何度も学習を繰り返して「慣れて」ください。そうすれば、多くの問題に共通した解法のポイントをつかめるはずです。
それでは、またお会いしましょう!
label 関連タグ
免除試験を受けた 74.9% の方が、科目A免除資格を得ています。
※独習ゼミは、受験ナビ運営のSEプラスによる試験対策eラーニングです。

具体的な値を入れるとプログラムがわかる練習問題|アルゴリズムとプログラミング問題を解くコツ
update
具体例からヒントを掴む練習問題|アルゴリズムとプログラミング問題を解くコツ
update
プログラムを分割するコツがわかる練習問題|アルゴリズムとプログラミング問題を解くコツ
update
手順をヒントにトレースする練習問題|アルゴリズムとプログラミング問題を解くコツ
update
トレースのテクニックが身につく練習問題|アルゴリズムとプログラミング問題を解くコツ
update
2進数を掛け算するプログラム | アルゴリズムとプログラミング問題を解くコツ
update
ヒープを配列で実現するプログラム|アルゴリズムとプログラミング問題を解くコツ
update
ルールに従って検査文字(チェックディジット)を求めるプログラム|アルゴリズムとプログラミング問題を解くコツ
update
配列のマッチング(突合せ)を行うプログラム|アルゴリズムとプログラミング問題を解くコツ
update
2進数の知識が必要なプログラム|アルゴリズムとプログラミング問題を解くコツ
update
『プログラムはなぜ動くのか』(日経BP)が大ベストセラー
IT技術を楽しく・分かりやすく教える“自称ソフトウェア芸人”
大手電気メーカーでPCの製造、ソフトハウスでプログラマを経験。独立後、現在はアプリケーションの開発と販売に従事。その傍ら、書籍・雑誌の執筆、またセミナー講師として活躍。軽快な口調で、知識0ベースのITエンジニアや一般書店フェアなどの一般的なPCユーザの講習ではダントツの評価。
お客様の満足を何よりも大切にし、わかりやすい、のせるのが上手い自称ソフトウェア芸人。
主な著作物
- 「プログラムはなぜ動くのか」(日経BP)
- 「コンピュータはなぜ動くのか」(日経BP)
- 「出るとこだけ! 基本情報技術者」 (翔泳社)
- 「ベテランが丁寧に教えてくれる ハードウェアの知識と実務」(翔泳社)
- 「ifとelseの思考術」(ソフトバンククリエイティブ) など多数










