2進数を掛け算するプログラム | アルゴリズムとプログラミング問題を解くコツ

科目 B 問題の新しい擬似言語に合わせて、プログラムを変更しました。
なお、本記事では過去問題を一部改変しています。
この連載では、基本情報技術者試験で、多くの受験者が苦手意識を持っている科目 B 試験 アルゴリズムとプログラミング分野の「アルゴリズム穴埋め問題」に的を絞って、正解を見出すポイントを詳しく説明します。
苦手を克服するには、短いプログラムを何度も練習して、穴埋めに慣れることが重要です。
そのために、実際の試験問題の一部をアレンジした練習問題を作りました。 とても短い問題ですので、気軽に取り組んでください。
もくじ
練習問題
関数 MUL は、二つの整数 M 、 N を受け取り、その積 M × N を返す。 積は、加算とシフト演算を使って求める。 M 、 N 及び求めた積は、いずれも符号付き 2 進数の整数で、負数は 2 の補数で表現する。
関数 MUL が受け取る M 、 N は、いずれも 4 ビットで、各値の範囲は -8 ~ 7 である。 求めた積 M × N は、 8 ビットで返す。 ただし、プログラム中では、 M を 5 ビットに、 N を 8 ビットに拡張して処理を行う。
R は、 13 ビットの作業用変数であり、最下位から順にビット番号を 0, 1, ・・・とし、最上位(符号ビット)のビット番号を 12 とする。 R は、指定した一部の範囲(例えば、ビット番号 12 ~ 8 の上位 5 ビット)だけを符号付き 2 進数とみなして部分的な算術演算ができる。 また、値の検査のために指定したビット番号の内容を取り出すこともできる。
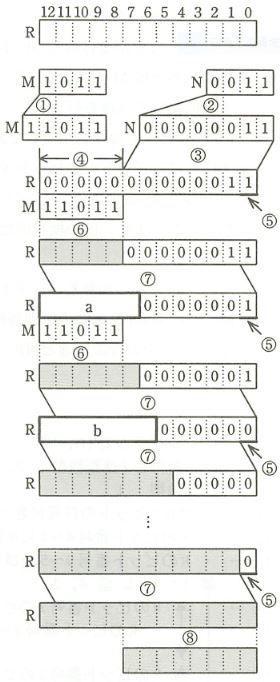
M = -5 、N = 3 の場合の処理過程を、図に示す。 図中の記号 ① ~ ⑧ は、プログラムの ① ~ ⑧ の行の処理と対応している。 なお、 ⑥ の行の加算では、けたあふれが起きても無視する。
[プログラム]
◯整数型: MUL(M, N)
符号付き 2 進整数型: M, N, R
整数型: L
M を 5 ビットの符号付き 2 進数に拡張
N を 8 ビットの符号付き 2 進数に拡張
R のビット番号 7 ~ 0 に N を複写
R のビット番号 12 ~ 8 を 0 で初期化
for (L を 1 から 8 以下まで 1 つずつ増やす)
if (R のビット番号 0 のビットが 1)
R のビット番号 12 ~ 8 の内容に M の値を加算
endif
R の全 13 ビットを右に 1 ビット算術シフト /* 空いたビット位置には符号と同じものが入る */
endfor
return (R のビット番号 7 ~ 0 の内容) /* 返却値(括弧内)を返す */❶❷❸❹❺❻❼❽
設問 プログラム中のに入れる正しい答えを、解答群の中から選べ。
a に関する解答群
ア  イ
イ 
ウ  エ
エ 
b に関する解答群
ア 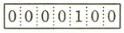 イ
イ 
ウ 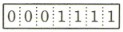 エ
エ 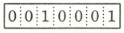
オ  カ
カ 
ポイント1:2進数の取り扱いに慣れておく
2 進数が苦手な人は、この問題を見て「すご~く難しそう!」と感じたでしょう。 それなら、この機会に、 2 進数の取り扱いに慣れておきましょう。
基本情報技術者試験の旧午後試験のアルゴリズム問題では、それほど頻度は多くありませんが、 2 進数を取り扱う問題が出ることがあったからです。 お手元の教材(きっと何らかの教材をお持ちでしょう)に示された 2 進数に関する知識を、丁寧に学習してください。
この問題を解くには、以下の知識が必要になります。 どれも基礎知識ですので、しっかりマスターしておいてください。
- 10 進数と 2 進数の変換
- 2 進数の加算
- 2 の補数表現
- 符号ビット
- 算術右シフト
- 符号拡張
searchタグで関連記事をチェック2 進数
ポイント2:符号拡張は、同じ値のままビット数を増やす
ちゃんと 2 進数の知識があれば、この問題は、決して難しくありません。 問題に示された数値を、問題に示された手順通りに、順番に処理していけばよいからです。
問題に示されたプログラムの内容は、プログラムというより、処理内容を説明した文書です。 それぞれの文書を読めば、処理内容がわかります。
プログラムの各行に付けられた ① ~ ⑧ は、穴埋めがある図に示された ① ~ ⑧ に対応しています。
それぞれに合わせて、問題に示された数値の変化を図の中に書き込んでいけば、穴埋めに入る数値がわかります。
それでは、やってみましょう。
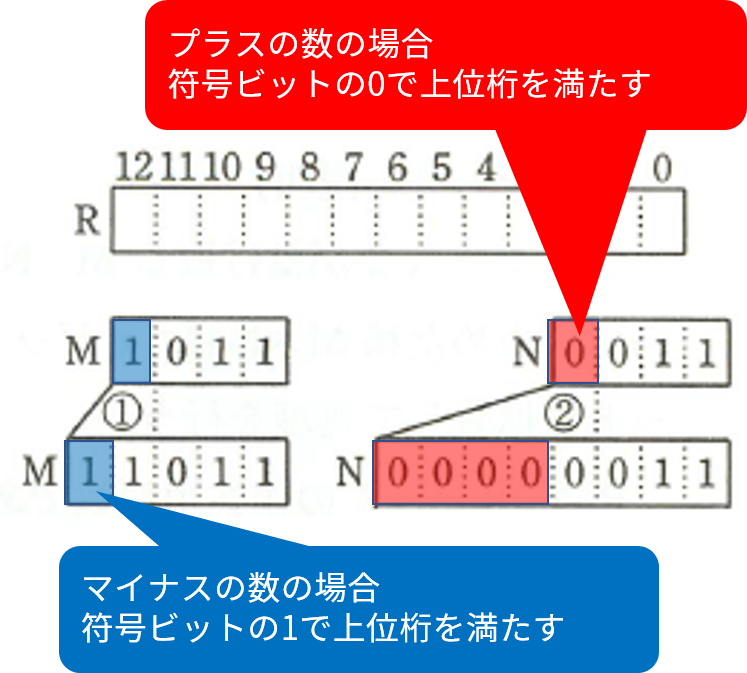
まず、 ① と ② です。 ここでは、符号拡張(問題文では「拡張」と呼んでいる)を行っています。 符号拡張とは、同じ値(符号も同じ)のままビット数を増やすことです。
ここでは、 2 の補数表現を使っているので、符号ビット(最上ビット)が
0 ならプラスの値であり、
1 ならマイナスの値です。
同じ値のままビット数を増やすには、増やした上位桁を、
プラスの値なら 0 で満たし、
マイナスの値なら 1 で満たします。
どちらの場合も、符号ビットを上位桁に「ぐい~ん」と拡張しているように見えるので、符号拡張と呼ぶのです。
ポイント3: 算術右シフトは、空いた上位桁に符号ビットと同じ値を入れる
次に、空欄 a があるところまで、数値の変化を見ていきましょう。
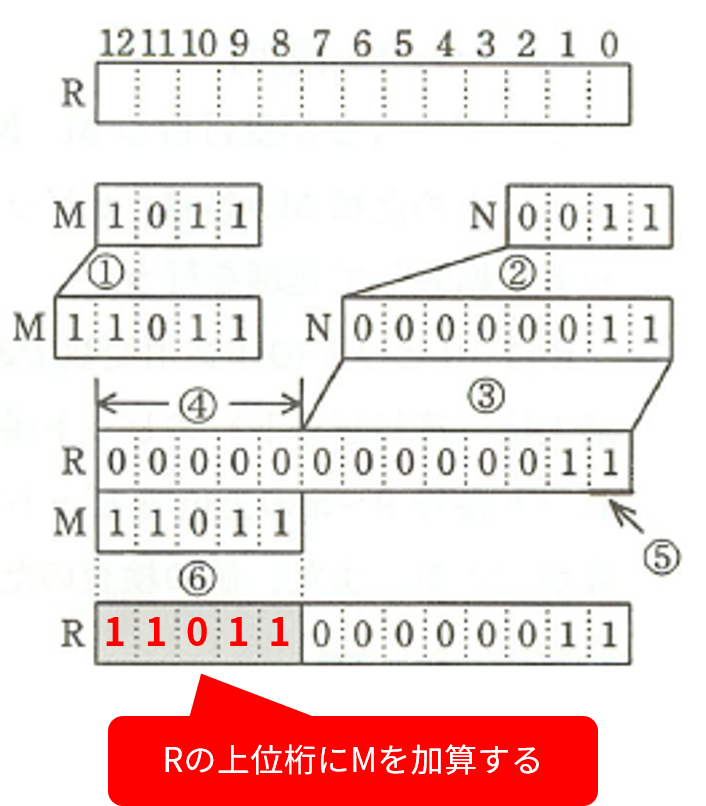
③ では、 R の下位桁に N を複写しています。
④ では、 R の上位桁を 0 で埋めています。
⑤ では、 R の最下位桁が 1 であることをチェックしています。
⑥ では、 R の上位桁に M を加算しています。
この時点では、 R の上位桁がすべて 0 なので、グレー表示になっている部分に、 M の値をそのまま入れれば OK です。 ここまでの手順には、特に難しいことはないでしょう。
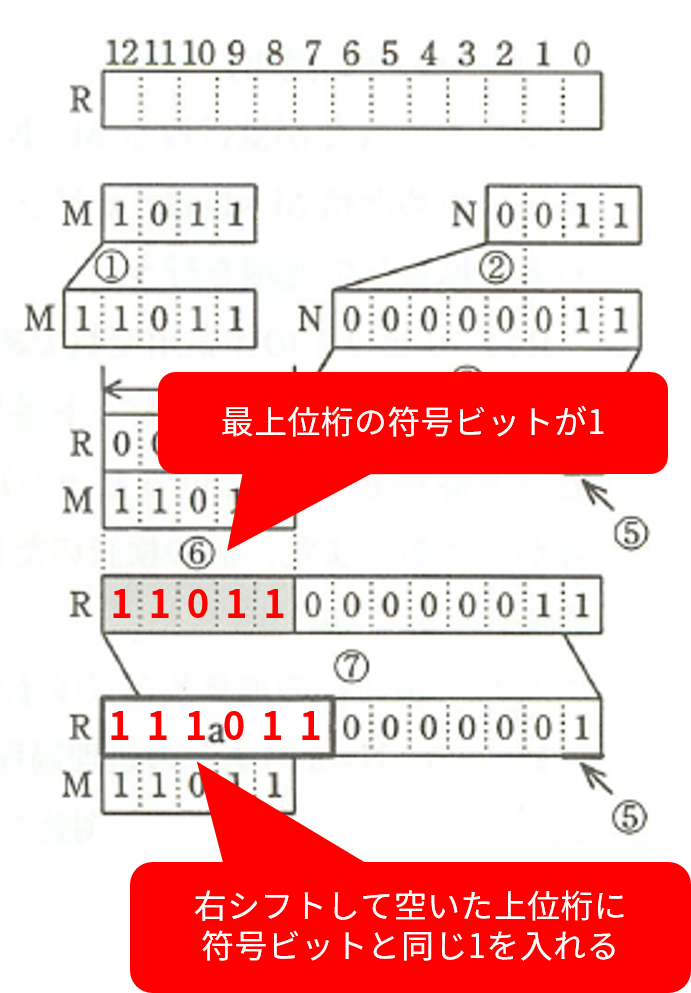
次の ⑦ では、 R の全ビットを右に 1 ビット算術シフトします。
「算術」シフトであることに注意してください。 右シフトすると、上位桁に空きができます。 算術シフトでは、ここに符号ビットと同じ値を入れます。 こうすることで、符号を変えずに、値を 1/2 にできます。
ここでは、シフト前の値が
1101100000011
なので、右に 1 ビット算術シフトすると、空いた上位桁に符号ビットと同じ値の 1 を入れて、
1110110000001
になります。
したがって、空欄 a は、 111011 であり、選択肢エが正解です。
ポイント4:2進数の加算は、2で桁上がりする
次の ⑥ では、 11101 と 11011 を加算します。
ここでは、 2 進数の加算なので、下位桁から加算を行って、結果が 2 になったら桁上がりすることに注意してください。
問題文に、最上位桁からの桁あふれは無視するとあるので、以下のように計算して、結果は 11000 になります。
11101
+ 11011
---------
11000
この 11000 を ⑥ の下のグレー表示になっている部分に入れ、次の ⑦ で右に 1 ビット算術シフトします。
先ほどと同様に、ここでも最上位桁の符号ビットが 1 なので、空いた上位桁に符号ビットと同じ 1 を入れて、空欄 b は、 1110001 になります。 正解は、選択肢オです。

解答a - エ, b - オ
「習うより慣れろ」ということわざがあります。 アルゴリズム穴埋め問題の克服に関しては、正にその通りでしょう。
この連載では、これからも短い練習問題を掲載していきますので、穴埋めに慣れることを目指してください。
正解を見出すポイントとして、同じことが示されることもあると思いますが、それは、多くの問題に共通したポイントがあるからです。
それでは、またお会いしましょう!
label 関連タグ免除試験を受けた 74.9% の方が、科目A免除資格を得ています。
※独習ゼミは、受験ナビ運営のSEプラスによる試験対策eラーニングです。

具体的な値を入れるとプログラムがわかる練習問題|アルゴリズムとプログラミング問題を解くコツ
update
具体例からヒントを掴む練習問題|アルゴリズムとプログラミング問題を解くコツ
update
プログラムを分割するコツがわかる練習問題|アルゴリズムとプログラミング問題を解くコツ
update
手順をヒントにトレースする練習問題|アルゴリズムとプログラミング問題を解くコツ
update
トレースのテクニックが身につく練習問題|アルゴリズムとプログラミング問題を解くコツ
update
2進数を掛け算するプログラム | アルゴリズムとプログラミング問題を解くコツ
update
ヒープを配列で実現するプログラム|アルゴリズムとプログラミング問題を解くコツ
update
ルールに従って検査文字(チェックディジット)を求めるプログラム|アルゴリズムとプログラミング問題を解くコツ
update
配列のマッチング(突合せ)を行うプログラム|アルゴリズムとプログラミング問題を解くコツ
update
2進数の知識が必要なプログラム|アルゴリズムとプログラミング問題を解くコツ
update
『プログラムはなぜ動くのか』(日経BP)が大ベストセラー
IT技術を楽しく・分かりやすく教える“自称ソフトウェア芸人”
大手電気メーカーでPCの製造、ソフトハウスでプログラマを経験。独立後、現在はアプリケーションの開発と販売に従事。その傍ら、書籍・雑誌の執筆、またセミナー講師として活躍。軽快な口調で、知識0ベースのITエンジニアや一般書店フェアなどの一般的なPCユーザの講習ではダントツの評価。
お客様の満足を何よりも大切にし、わかりやすい、のせるのが上手い自称ソフトウェア芸人。
主な著作物
- 「プログラムはなぜ動くのか」(日経BP)
- 「コンピュータはなぜ動くのか」(日経BP)
- 「出るとこだけ! 基本情報技術者」 (翔泳社)
- 「ベテランが丁寧に教えてくれる ハードウェアの知識と実務」(翔泳社)
- 「ifとelseの思考術」(ソフトバンククリエイティブ) など多数










