過去問の解き方知りたいぜ | よく出る「鉄板問題」を解説

基本情報技術者試験には、頻繁に出題されている問題がいくつかあります。それらの中には、あらかじめ十分に練習しておかないと解けない問題もあります。
ここでは、そのような問題を 「鉄板問題」 と呼び、解き方のポイントを説明します。
午前試験の過去問題を例として取り上げますが、午後試験の対策にもなるはずです。午後試験の問題は、午前試験の知識を事例に仕立てたものだからです。
もくじ
全 19 回中 16 回も出題された問題がある
拙著「情報処理教科書 出るとこだけ!基本情報技術者 テキスト&問題集 2019 年版」(翔泳社刊)」の中には、「試験によく出る問題と用語 Top 100 」という資料が掲載されています。
これは、現行の試験制度になった平成 21 年度 春期から平成 30 年度 春期までの全 19 回の午前試験を、独自に調査したものです。
以下は、それらの中から 10 回以上( 50 % 以上)の頻度で出題された問題を抜粋したものです。
| 順位 | 回数 | テーマ | 分野 |
|---|---|---|---|
| 1 位 | 16 回 |
|
|
| 2 位 | 13 回 | リピータ、ブリッジ、ルータの説明 | T |
| 3 位 | 12 回 |
|
|
| 4 位 | 11 回 | 著作権の対象 | S |
| 5 位 | 10 回 | 再帰呼び出しの仕組み | T |
何とビックリ! 全 19 回中 16 回(約 84 % )も出題された問題があります。
- MIL 記号による論理演算
- アローダイアグラムの使い方
- 稼働率の計算
というテーマの問題です。これらは、あらかじめ十分に練習しておかないと解けないので、正に「鉄板問題」だといえます。
絶対に解き方を覚えておくべきです。例題を示しますので、一緒にやってみましょう。
「 MIL 記号による論理演算」の例題と解説
最初に紹介する鉄板問題は、「 MIL 記号 による論理演算」です。
「 MIL 記号(ミルきごう)」とは、AND や OR などの論理演算を行う電子回路を図示する記号で、米国の軍事規格( MIL は、military = 軍事という意味)で定められたものです。
午前試験の問題用紙の冒頭に、MIL 記号 が一覧表示されていますが、よく出題される AND、OR、XOR、NOT、NAND、NOR の MIL 記号 は、あらかじめ覚えておきましょう。
| 図記号 | 説明 |
|---|---|
| 論理積素子( AND ) | |
| 否定論理積素子( NAND ) | |
| 論理和素子( OR ) | |
| 否定論理和素子( NOR ) | |
| 排他的論理和素子( XOR ) | |
| 論理一致素子 | |
| バッファ | |
| 論理否定器( NOT ) | |
| スリーステートバッファ |
MIL 記号 は、難しそうに見えますが、オデンの具だと思えば可愛いものです。
AND ![]() は、カマボコです。
は、カマボコです。
OR ![]() は、サツマアゲです。
は、サツマアゲです。
XOR ![]() は、サツマアゲをかじったものです。
は、サツマアゲをかじったものです。
NOT ![]() は、コンニャクの先にギンナンが付いたものです。
は、コンニャクの先にギンナンが付いたものです。
このギンナン(小さな白丸)は、データを反転( 0 を 1 に、1 を 0 に)することを意味します。
カマボコの先にギンナンを付けると、AND の反転で NAND ![]() になります。
になります。
サツマアゲの先にギンナンを付けると、OR の反転の NOR ![]() になります。
になります。
どの MIL 記号にも、ご丁寧に串が刺してあります。この串 1 本で、1 ビットのデータが伝えられます。
図記号の左側から入力されたデータが、素子の中で論理演算され、その結果が右側から出力されます。
以下は、「 MIL 記号 による論理演算」の例題(平成 28 年度 春期 問 23 )です。
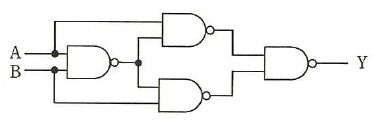
問題に示された論理回路は、NAND を組合わせて作られていますが、この論理回路は、選択肢に示された OR(ア)、AND(イ)、XOR(ウ)、NOR(エ)と同じ機能になります。
様々な論理演算を NAND を組合わせた論理回路で実現することを「 NAND 変換」と呼びます。
図の論理回路と等価な回路はどれか。
ア 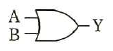 イ
イ 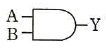 ウ
ウ 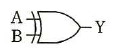 エ
エ 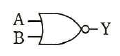
「 MIL 記号による論理演算」の問題には、効率的に解く方法(回路図や演算式を変形してシンプルにする方法)がある場合がありますが、少し時間がかかっても確実に解ける方法は、 具体的なデータを想定すること です。
論理演算 (論理回路) 問題の解き方
具体的なデータを想定する ( 1 つのデータで選択肢を絞れない場合は、別のデータを想定する)
この問題に示された論理回路には、A と B という 2 つの入力があって、Y という 1 つの出力があります。
A と B に具体的なデータを想定して、Y が何になるかを調べてみましょう。
選択肢の中で、それと同じ結果にならないものを消していって、残ったものが正解です。1 つのデータでは、選択肢を 1 つに絞れないなら、別のデータで調べてください。
まず、A に 0 、B に 1 というデータを想定してみましょう。
以下のように、Y の値は、1 になります。この結果は、イ の AND と エ の NOR と同じではないので、答えをアの OR と、ウの XOR に絞れます。
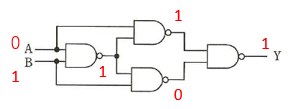
OR と XOR の違いは、2 つの入力の両方が 1 のとき、OR では 結果が 1 になりますが、XOR では 結果が 0 になることです。
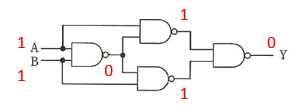
そこで、A に 1 、B に 1 というデータを想定してみましょう。
以下のように、Y の値は、0 になります。この結果は、アの OR とは違うので、答えをウの XOR に絞れます。実際の正解も ウ です。
label関連タグ論理回路
「アローダイアグラムの使い方」の例題と解説
次に紹介する鉄板問題は、「アローダイアグラムの使い方」です。
「アローダイアグラム( arrow diagram = 矢印の図)」とは、プロジェクトを構成する作業の流れを示したものです。
以下は、例題(平成 23 年度 秋期 問 51 )です。矢印で作業を示します。
矢印に添えられた A 、B 、C などは 作業名 であり、3 、2 、1 などは 作業の所要日数 です。作業と作業のつなぎ目を「結合点」と呼び、円で示します。円の中にある数字は、結合点の番号です。
破線で示された矢印は、「ダミー作業」と呼ばれ、そこに 所要日数 0 日の作業がある と考えます。作業のつなぎ方によって、ダミー作業が必要になる場合があります。
問題を解くときに、ダミー作業に 0 という数字を書き添えるとよいでしょう。
次のアローダイアグラムで表されるプロジェクトがある。結合点 5 の最早結合点時刻は第何日か。
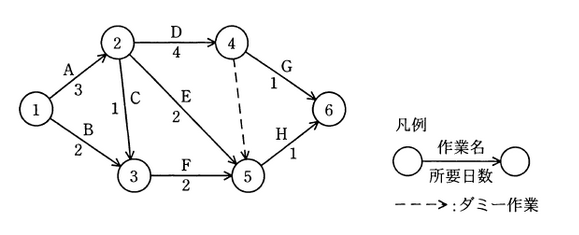
ア 4 イ 5 ウ 6 エ 7
アローダイアグラムから求められるのは、「プロジェクトが最短で何日で完了するか」と「クリティカルパス( critical path = 重要な道筋)」です。
まず、図を左から右に(スタートからゴールに向かって)たどって、それぞれの結合点に「最早結合点時刻(最も早くて、いつから始められるか)」を書き込んでいくと、「プロジェクトが最短で何日で完了するか」を求められます。
次に、図を右から左に(ゴールからスタートに向かって)たどって、それぞれの結合点に「最遅結合点時刻(最も遅くて、いつまでに始めなければならないか)」を書き込んでいくと、「クリティカルパス」を求められます。
アローダイアグラム問題の解き方
- 結合点ごとに「最早結合点時刻」「最遅結合点時刻」を書き込める箱を2つ書いておく
- アローダイアグラムの図の左から右へたどって、結合点に「最早結合点時刻」を図に書き込む -> 最短完了日
- アローダイアグラムの図の右から左へたどって、結合点に「最遅結合点時刻」を図に書き込む -> クリティカルパス
- ダミー作業には 0 を書く
この問題は、結合点 5 の最早結合点時刻を求めるものですが、せっかくなので、「プロジェクトが最短で何日で完了するか」と「クリティカルパス」も求めてみましょう。
それぞれの結合点に 2 段重ねの四角形を書いてください。
この四角形の下段に 最早結合点時刻 を書き込み、上段に 最遅結合点時刻 を書き込みます(上下が逆でも問題ありません)。両者が同じになる作業は、余裕がありません。
「最も早くて、いつから始められるか」と「最も遅くて、いつまでに始めなければならないか」が同じ なら、作業の開始日にまったく余裕がないからです。
余裕のない作業を結んだ道筋がクリティカルパスです。クリティカルパスは、プロジェクトが完了するまでの日数を左右する「重要な道筋」です。
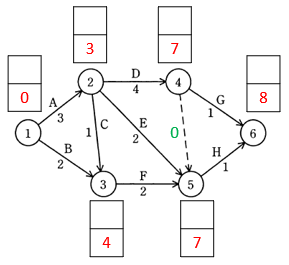
以下は、図を左から右にたどって、それぞれの結合点に 最早結合点時刻 を書き込んだものです。
1 つ前の作業が終わってから、次の作業を始めます。
複数の作業の終わりを待つ場合は、最も遅い作業の終わりを待ってから、次の作業を始めることに注意してください。プロジェクトのゴールとなっている結合点 6 の 最早結合点時刻 は、8 です。
したがって、このプロジェクトは、最短で 8 日間で完了します。結合点 5 の 最早結合点時刻 は、7 なので、この問題の答えは、エです。
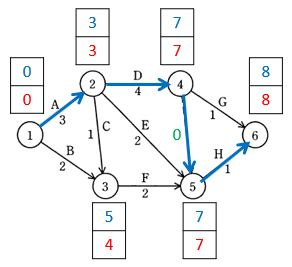
以下は、最早結合点時刻 を書き込んだ後の図を右から左にたどって、それぞれの結合点に 最遅結合点時刻 を書き込んだものです。
1つ先にある作業の 最遅結合点時刻 から逆算して、その前の作業の 最遅結合点時刻 を求めます。
複数の作業の起点となっている結合点の場合は、それらの中で最も早く始めなければならない作業を、最遅結合点時刻 とすること に注意してください。
ここでは、最早結合点時刻 と 最遅結合点時刻 が同じになる余裕のない作業を、わかりやすいように太線の矢印で示しています。
余裕のない作業を結んだクリティカルパスは、A → D →( ダミー作業 )→ H です。
label関連タグアローダイアグラム
「稼働率の計算」の例題と解説
最後に紹介する鉄板問題は、「稼働率の計算」です。
「稼働率」とは、システムが動作している確率です。試験には、複数の装置から構成されたシステムの稼働率を求める問題が、よく出題されます。
この手の問題を解くためには、基礎知識として
- それぞれの装置が 1 つだけしかなく、すべてが動作していなければならないシステムの稼働率を求める方法
- 同じ装置が複数あって、いずれか 1 つが動作していればよいシステムの稼働率を求める方法
この 2 つを覚えればOKです。
シンプルな例を示しましょう。
稼働率が 90 % のパソコン 1 台と、稼働率が 80 % のプリンタ 1 台から構成されたシステムがあるとします(実際には、こんなに稼働率が低いことはないと思いますが、計算しやすい値にしています)。
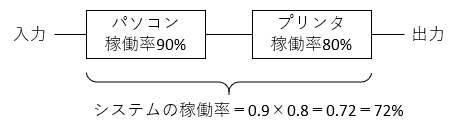
このシステムを図示すると、以下のように装置を直列につないだものになります。
装置と装置をつなぐ線は、その線をデータが流れて行くことを示します。
パソコンに入力されたデータの 90 % が出力され、それがプリンタに受け渡され、90 % の 80 % の 72 % が出力されます。
したがって、装置を直列につないだシステムの稼働率は、それぞれの装置の稼働率を掛け合わせて、
90 % × 80 % = 0.9 × 0.8 = 0.72 = 72 %
という計算で求められます。
稼働率が 80 % のプリンタが 2 台ある場合は、どうなるでしょう。
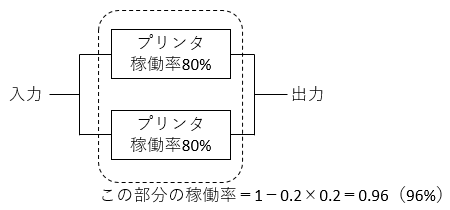
これを図示すると、以下のように装置を並列につないだものになります。
いずれかのプリンタが動作していれば、データを出力できます。その確率は、100 % から両方のプリンタが同時に止まる確率を引いたものです。
80 % で動作するプリンタは、100 % - 80 % = 20 % の確率で止まります。
2 台のプリンタが同時に止まる確率は、20 % × 20 % = 0.2 × 0.2 = 0.04 = 4% です。
したがって、いずれかのプリンタが動作している確率は、100 % - 4% = 96% です。
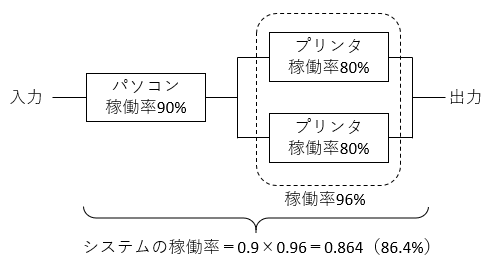
それでは、稼働率 90 % のパソコン 1 台と、稼働率 80 % のプリンタ 2 台から構成されたシステムの稼働率は、いくつになるでしょう。
以下のように、パソコンの部分が 90 % で、プリンタの部分が 96 % なので、
90 % × 96 % = 0.9 × 0.96 = 0.864 = 86.4 %
になります。ここまでの計算ができるようになれば、「稼働率の計算」の問題を解けるはずです。
それでは、過去問題を解いてみましょう。
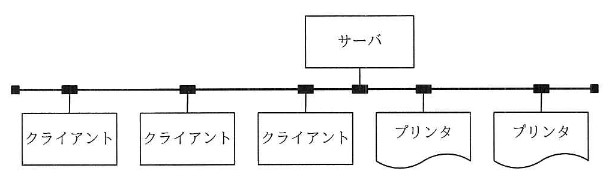
以下は、稼働率 a のサーバ 1 台、稼働率 b のクライアント 3 台、稼働率 c のプリンタ 2 台から構成されたシステムの稼働率を求める問題(平成 28 年度 春期 問 14 )です。稼働率 1 = 100 % の LAN は、常に動作しているので、計算に入れる必要はありません。
図のように,1 台のサーバ,3 台のクライアント及び 2 台のプリンタが LAN で接続されている。このシステムはクライアントからの指示に基づいて,サーバにあるデータをプリンタに出力する。各装置の稼働率が表のとおりであるとき,このシステムの稼働率を表す計算式はどれか。ここで,クライアントは 3 台のうちどれか 1 台が稼働していればよく,プリンタは 2 台のうちどちらかが稼働していればよい。
| 装置 | 稼働率 |
|---|---|
| サーバ | a |
| クライアント | b |
| プリンタ | c |
| LAN | 1 |
ア ab3c2 イ a( 1 – b3 )( 1 – c2 )
ウ a( 1 – b3 )( 1 – c )2 エ a( 1 – ( 1 – b3 )( 1 – ( 1 – c )2 )
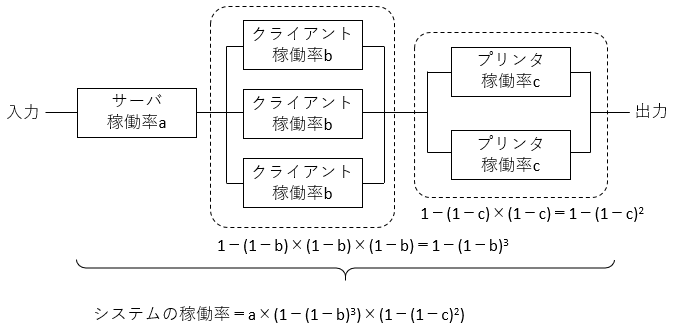
以下は、このシステムの構成を図示して、クライアントが 3 台ある部分と、プリンタが 2 台ある部分の稼働率を求め、さらにシステムの稼働率を求めたものです。選択肢にあるエと同じ式になっています。実際の正解もエです。
label関連タグ稼働率
過去問で腕試し
腕試しとして、この記事で紹介した以外の過去問題も解いてみてください。
以下に、鉄板問題が出題された年度と問題番号を示します。該当ページにリンクしていますので、そのページ内にある問題にチャレンジしてみてください。
いかがでしたか。鉄板問題の解法のポイントを、ご理解いただけたでしょう。
それでは、またお会いしましょう!
label 関連タグ
免除試験を受けた 74.9% の方が、科目A免除資格を得ています。
※独習ゼミは、受験ナビ運営のSEプラスによる試験対策eラーニングです。

『プログラムはなぜ動くのか』(日経BP)が大ベストセラー
IT技術を楽しく・分かりやすく教える“自称ソフトウェア芸人”
大手電気メーカーでPCの製造、ソフトハウスでプログラマを経験。独立後、現在はアプリケーションの開発と販売に従事。その傍ら、書籍・雑誌の執筆、またセミナー講師として活躍。軽快な口調で、知識0ベースのITエンジニアや一般書店フェアなどの一般的なPCユーザの講習ではダントツの評価。
お客様の満足を何よりも大切にし、わかりやすい、のせるのが上手い自称ソフトウェア芸人。
主な著作物
- 「プログラムはなぜ動くのか」(日経BP)
- 「コンピュータはなぜ動くのか」(日経BP)
- 「出るとこだけ! 基本情報技術者」 (翔泳社)
- 「ベテランが丁寧に教えてくれる ハードウェアの知識と実務」(翔泳社)
- 「ifとelseの思考術」(ソフトバンククリエイティブ) など多数













