ヒープを配列で実現するプログラム｜アルゴリズムとプログラミング問題を解くコツ

矢沢 久雄
2022-11-28 更新

この連載では、基本情報技術者試験で、多くの受験者が苦手意識を持っている科目 B 試験 アルゴリズムとプログラミング分野の「アルゴリズム穴埋め問題」に的を絞って、正解を見出すポイントを詳しく説明します。

苦手を克服するには、短いプログラムを何度も練習して、穴埋めに慣れることが重要です。

そのために、実際の試験問題の一部をアレンジした練習問題を作りました。 とても短い問題ですので、気軽に取り組んでください。

練習問題

問 8 (平成 30 年度 春期 午後）を一部改変

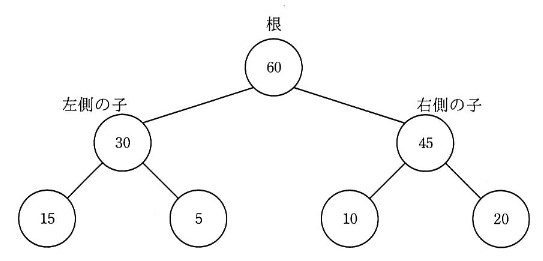
手続 makeHeap は、配列 data に格納されている hnum 個（ hnum > 0 ）のデータを、次の (1) ～ (3) の規則で配列 heap に格納して、ヒープを配列で実現する。 配列の添字は、 0 から始まる。

(1)

heap[i] ( i = 0, 1, 2, ・・・) は、ヒープの節に対応する。

(2)

heap[0] は、根に対応する。

(3)

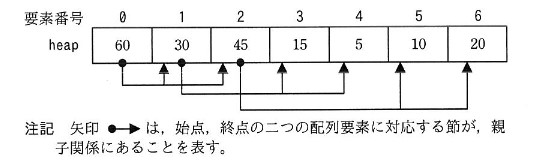
heap[i] ( i = 0, 1, 2, ・・・) に対応する節の左側の子は heap[2 × i + 1] に対応し、右側の子は heap[2 × i + 2] に対応する。 子が一つの場合、左側の子として扱う。

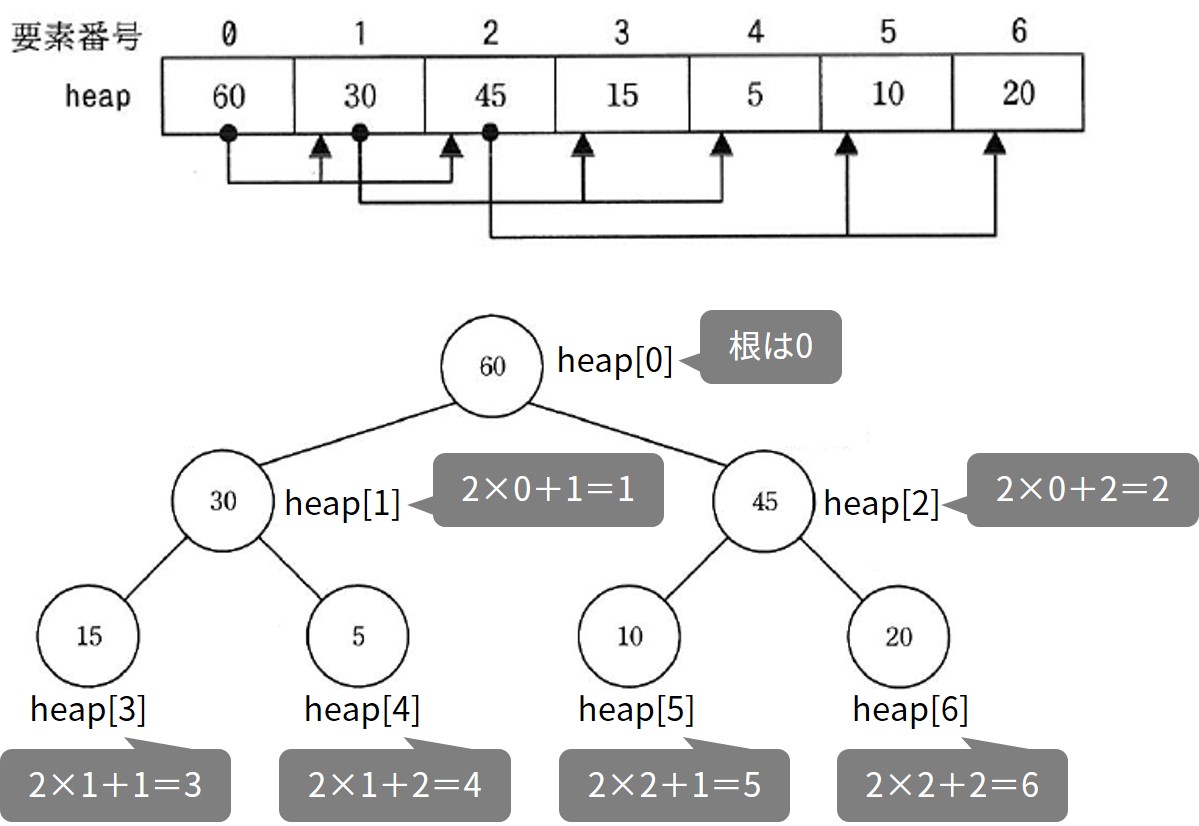
ヒープの例を図 1 に、図 1 に対応する配列 heap の例を図 2 に示す。

swipeアルゴリズムは横スクロールできます

［プログラム］

◯makeHeap(整数型の配列: data, 整数型の配列: heap, 整数型: hnum)
  整数型: i, k

  for (i が 0 から hnum より小さい間 1 ずつ増やす)
    heap[i] ← data[i]	/* heap にデータを追加 */
    k ← i

    while ( k が 0 より大きい)
      if ( a )
        swap(heap, k, b )
        k ← parent(k)
      elseif
        break		/* 内側の繰り返し処理から抜ける */
      endif
    endwhile
  endfor

設問

プログラム中のに入れる正しい答えを、解答群の中から選べ。

• プログラムおよび解答群の中で使われている関数 lchild( 整数型: k ) は、添字 k の配列要素に対応する節の左側の子の添字 2 × k + 1 を戻り値として返す。
• 関数 rchild( 整数型: k ) は、添字 k の配列要素に対応する節の右側の子の添字 2 × k + 2 を戻り値として返す。
• 関数 parent( 整数型: k ) 関数は、添字 k の配列要素に対応する親の添字 ( k – 1 ) ÷ 2 （小数点以下切捨て）を戻り値として返す。
• 関数 swap( 整数型: heap[], 整数型: i, 整数型: j ) は、 heap[i] と heap[j] の値を交換する。

a に関する解答群

ア

heap[k] が heap[lchild(k)] より大きい

イ

heap[k] が heap[parent(k)] より大きい

ウ

heap[k] が heap[rchild(k)] より大きい

エ

heap[k] が heap[lchild(k)] より小さい

オ

heap[k] が heap[parent(k)] より小さい

カ

heap[k] が heap[rchild(k)] より小さい

b に関する解答群

ア　heap[hnum - 1]
イ　heap[k]
ウ　parent(hnum - 1)
エ　parent(k)

ポイント1: シラバスに示されたアルゴリズムとデータ構造を知っておこう

この問題を見て「ヒープって何だろう？」と思った人は、試験の出題範囲の学習が不足しています。 IPA（情報処理推進機構）の Web ページから試験の出題範囲の細目を示した シラバス という資料を入手できます。

これを見ると、「代表的なアルゴリズム」および「データ構造の種類」として、以下が出題範囲であることが示されています。 ここには、ちゃんと「ヒープ」という言葉があります。

【代表的なアルゴリズム】

looks_one 整列・併合・探索のアルゴリズム

整列のアルゴリズム、併合のアルゴリズム、探索のアルゴリズムの基本的な設計方法を理解する。

用語例選択ソート、バブルソート、マージソート、挿入ソート、シェルソート、クイックソート、ヒープソート、線形探索法、 2 分探索法、ハッシュ表探索法

looks_two 再帰のアルゴリズム

再帰的アルゴリズムの基本を理解する。

looks_3 グラフのアルゴリズム

グラフのアルゴリズムの基本を理解する。

用語例深さ優先探索、幅優先探索、最短経路探索

looks_4 文字列処理のアルゴリズム

文字列処理のアルゴリズムの基本を理解する。

用語例文字列照合

looks_5 ファイル処理のアルゴリズム

バッチ処理などで用いる整列処理、併合処理、コントロールブレーク処理、編集処理の基本を理解する。

【データ構造の種類】

looks_one 配列

配列の特徴、基本的な操作を理解する。

用語例多次元配列、静的配列、動的配列

looks_two リスト

リストの基本的な考え方、その操作を理解する。

用語例線形リスト、単方向リスト、双方向リスト、環状リスト

looks_3 スタックとキュー

スタックとキューの特徴、基本的な操作を理解する。

用語例FIFO 、LIFO 、プッシュ、ポップ

looks_4 木構造

木構造の種類と特徴、木の巡回法、節の追加や削除、ヒープの再構成などを理解する。

用語例根、葉、枝、 2 分木、完全 2 分木、バランス木、順序木、多分木、探索木、 2 分探索木、深さ優先探索、幅優先探索、先行順、後行順、中間順

アルゴリズムに「ヒープソート」があり、データ構造に「ヒープ」があるからこそ、この問題が出題されたのです。

ヒープに限らず、もしもシラバスの中に知らないアルゴリズムやデータ構造があったら、教材（きっと何らかの教材をお持ちでしょう）で学習してください。

すべてを詳細に理解する必要はありませんが、少なくとも、それが何であるかは、わかるようにしておきましょう。

ポイント2: ヒープのデータ構造を知っておこう

ヒープは、1 つのデータが枝分かれして 2 つのデータにつながる 2 分木の一種です。

ヒープを図示するときには、慣例として、データを円で囲んで示し、円を線で結んでデータのつながりを示します。

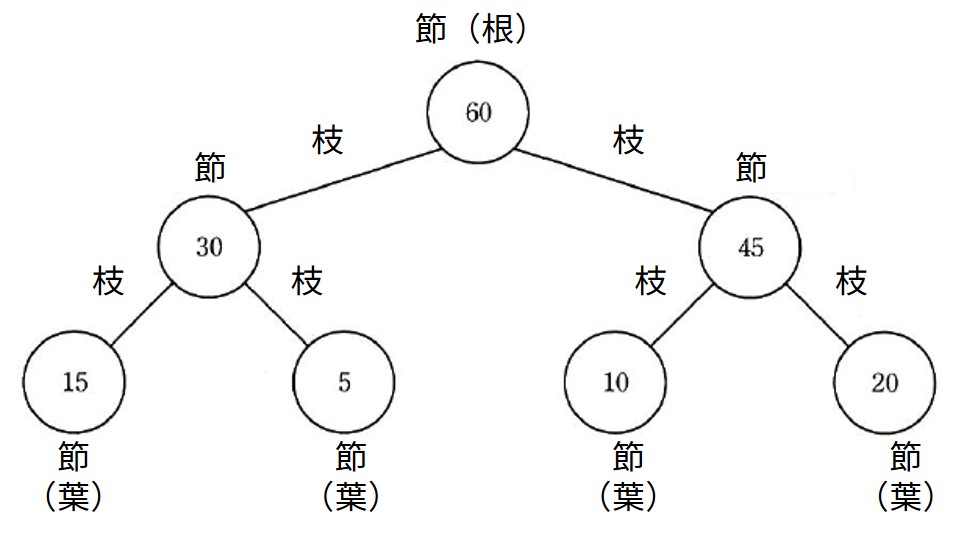
データを「節（ノード）」と呼び、線を「枝（ブランチ）」と呼びます。
枝分かれの元にある節を「親」と呼び、枝分かれの先にある節を「子」と呼びます。
最上部にある節を「根（ルート）」と呼びます。
最下部にあり枝がない節を「葉（リーフ）」と呼ぶこともあります。

どれも、自然界の木の構成要素を示す名称と同じです。

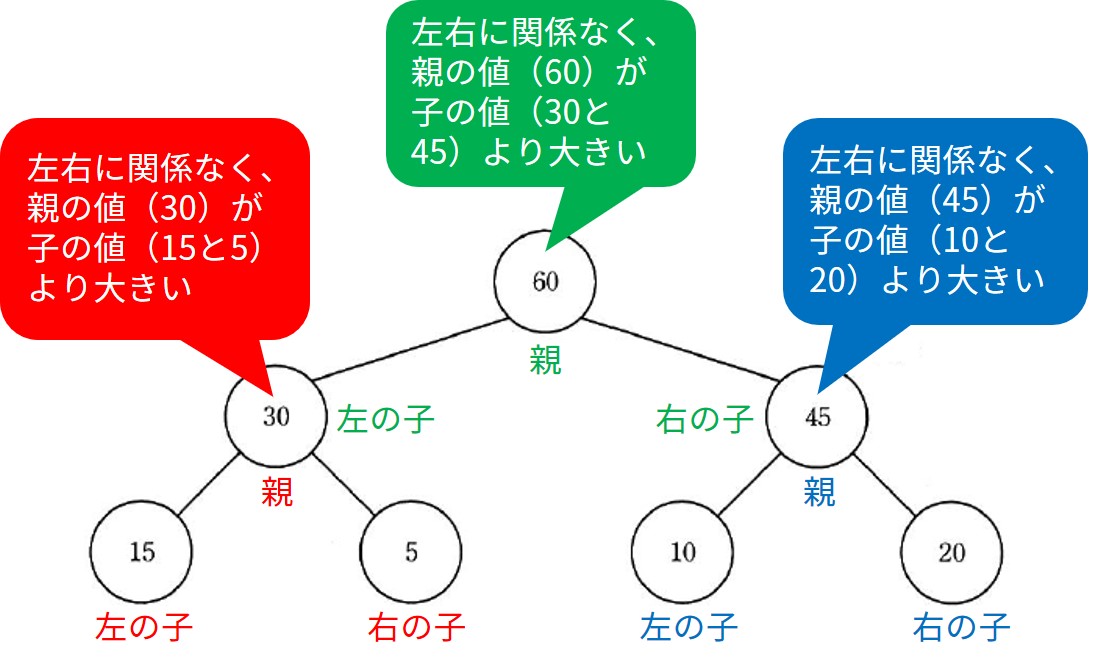
ヒープでは、
「左右に関係なく、親の値が子の値より小さい」とする場合と、
「左右に関係なく、親の値が子の値より大きい」とする場合があります。

この問題では、後者になっています。

ヒープに限らず、どのようなデータ構造でも、それをプログラムで実現するときには、配列が使われます。

ここでは、問題に示された (1) ～ (3) の規則で、ヒープを配列で実現しています。

ポイント3: ヒープを作成する手順を知っておこう

この問題を解くには、ヒープのデータ構造だけでなく、ヒープを作成する手順を知っていなければなりません。 問題に示された手続 makeHeap は、配列 data に格納された hnum 個の要素を、ヒープの形式で配列 heap に格納するものだからです。

ヒープは、以下の (1) ～ (3) の手順で作成できます。

ここでは、かなり大雑把に手順を示しています。 新たな要素を仮に格納してから、要素を交換して、適切な位置に移動させることがポイントです。

1. 配列 data の要素を先頭から 1 つずつ順番に取り出し、それを配列 heap の同じ位置に仮に格納する。
2. 配列 heap に新たに格納した要素が、親の要素より大きいなら、両者を交換することを根に達するまで繰り返す（親の要素より大きくない時点で、繰り返しを途中終了することもある）。
3. 1. と 2. を配列要素の末尾まで繰り返す。

ヒープを作成する手順がわかったら、問題の穴埋めができます。

以下は、手順に合わせたコメントをプログラムに追加したものです。 コメントは、 aとbがある部分まで付けています。

◯makeHeap(整数型の配列: data, 整数型の配列: heap, 整数型: hnum)
  整数型: i, k

  for (i が 0 から hnum より小さい間 1 ずつ増やす) /* 配列 data の要素を先頭から末尾まで処理する */
    heap[i] ← data[i]                           /* 配列 data の要素を、配列 heap の同じ位置に仮に格納する */
    k ← i                                       /* 新たに格納した要素の添字を k に格納する */

    while ( k が 0 より大きい)                    /* k が 0 （根）にたどり着くまで繰り返す */
      if ( a )                         /* aが真なら関数 swap で交換処理をする */
        swap(heap, k, b )              /* heap[k] と heap[b] を交換する */
        k ← parent(k)
      elseif
        break
      endif
    endwhile
  endfor

関数 swap で交換処理をするのは「子が親より大きい」という条件が真の場合です。

ここでは、子が heap[k] であり、その親の添字は関数 parent(k) で求められるので、「子が親より大きい」という条件は、

heap[k] が heap[parent(k)] より大きい

になります。 したがって、aは選択肢イが正解です。

関数 swap で交換するのは、 heap[k] と heap[parent(k)] です。 関数 swap の引数には、交換する要素の添字を指定するので、bは parent(k) であり、選択肢エが正解です。

いかがでしょうか？

ヒープのデータ構造と、ヒープの作成方法を知っていれば、とっても簡単な穴埋め問題だったはずです。 繰り返しアドバイスしますが、もしもシラバスの中に知らないアルゴリズムやデータ構造があったなら、教材で学習してください。

シラバスに示されていることは「知っているよね！」というノリで出題されるからです。

解答a – イ, b – エ

「習うより慣れろ」ということわざがあります。 アルゴリズム穴埋め問題の克服に関しては、正にその通りでしょう。

この連載では、これからも短い練習問題を掲載していきますので、穴埋めに慣れることを目指してください。

正解を見出すポイントとして、同じことが示されることもあると思いますが、それは、多くの問題に共通したポイントがあるからです。

それでは、またお会いしましょう！

具体的な値を入れるとプログラムがわかる練習問題｜アルゴリズムとプログラミング問題を解くコツ

update 2022-11-28

具体例からヒントを掴む練習問題｜アルゴリズムとプログラミング問題を解くコツ

update 2022-11-28

プログラムを分割するコツがわかる練習問題｜アルゴリズムとプログラミング問題を解くコツ

update 2022-11-28

手順をヒントにトレースする練習問題｜アルゴリズムとプログラミング問題を解くコツ

update 2022-11-28

トレースのテクニックが身につく練習問題｜アルゴリズムとプログラミング問題を解くコツ

update 2022-11-28

2進数を掛け算するプログラム | アルゴリズムとプログラミング問題を解くコツ

update 2022-11-28

ヒープを配列で実現するプログラム｜アルゴリズムとプログラミング問題を解くコツ

update 2022-11-28

ルールに従って検査文字（チェックディジット）を求めるプログラム｜アルゴリズムとプログラミング問題を解くコツ

update 2022-11-28

配列のマッチング（突合せ）を行うプログラム｜アルゴリズムとプログラミング問題を解くコツ

update 2022-11-28

2進数の知識が必要なプログラム｜アルゴリズムとプログラミング問題を解くコツ

update 2022-11-28

矢沢 久雄

『プログラムはなぜ動くのか』（日経BP）が大ベストセラー
IT技術を楽しく・分かりやすく教える“自称ソフトウェア芸人”

大手電気メーカーでＰＣの製造、ソフトハウスでプログラマを経験。独立後、現在はアプリケーションの開発と販売に従事。その傍ら、書籍・雑誌の執筆、またセミナー講師として活躍。軽快な口調で、知識０ベースのＩＴエンジニアや一般書店フェアなどの一般的なＰＣユーザの講習ではダントツの評価。
お客様の満足を何よりも大切にし、わかりやすい、のせるのが上手い自称ソフトウェア芸人。

主な著作物

• 「プログラムはなぜ動くのか」（日経BP）
• 「コンピュータはなぜ動くのか」（日経BP）
• 「出るとこだけ! 基本情報技術者」 (翔泳社)
• 「ベテランが丁寧に教えてくれる ハードウェアの知識と実務」（翔泳社）
• 「ｉｆとｅｌｓｅの思考術」（ソフトバンククリエイティブ）　など多数