「厳選5題」過去問と解説 | 平成22年度 春期 の過去問やるならこれをやれ

ここでは、平成 22 年度 春期 基本情報技術者試験の午前試験 の中から「やるべき問題」を 5 題に厳選し、ぶっちゃけた解説をさせていただきます。
やるべき問題とは、よく出る問題であり、かつ、練習すればできる問題(練習しないとできない問題)です。
もくじ
【厳選問題 1 】
CPU がカチカチ信号で動作しているイメージをつかもう
表の CPI と構成比率で,3 種類の演算命令が合計 1,000,000 命令実行されるプログラムを,クロック周波数が 1 GHz のプロセッサで実行するのに必要な時間は何ミリ秒か。
| 演算命令 | CPI ( Cycles Per Instruction ) | 構成比率 ( % ) |
|---|---|---|
| 浮動小数点加算 | 3 | 20 |
| 浮動小数点乗算 | 5 | 20 |
| 整数演算 | 2 | 60 |
ア 0.4 イ 2.8 ウ 4.0 エ 28.0
「クロック周波数」や「 CPI 」という言葉をご存知ですか? ご存知でないなら、この問題で覚えてください。
コンピュータの演算制御装置であるプロセッサ( CPU とも呼びます)は、時計のようにカチカチと繰り返される電気信号で動作していて、これをクロック信号と呼びます。
1 秒間にプロセッサに与えられるクロック信号の数をクロック周波数と呼びHz(ヘルツ)という単位で示します。
たとえば、クロック周波数が 1 GHz なら、1 秒間に 1 G 個= 1 × 109 個のクロック信号がプロセッサに与えられます。
プロセッサが解釈・実行する命令は、命令の種類によって何個のクロック信号が必要なのかが決まっていて、これをCPI( Cycles Per Instruction )という単位で示します。
たとえば、3 個のクリック信号で解釈・実行できる命令の CPI は、3 です。ここまでが、この問題を解くために必要な知識です。
それでは、問題を解いてみましょう。
3 種類の演算命令があり、それぞれ CPI の値が異なります。ここでは、命令の構成比率(プログラムの中で使われている比率)が示されているので、3 つの命令を平均した CPI は、
になります。
プログラムの中には、全部で 1000000 命令あるので、プログラムを実行するのに必要はクロック数は、全部で
です。
これを 1 GHz のクロック周波数、つまり 1 秒間に 1 G 個= 1 × 109 個のクロック信号が与えられるプロセッサで実行するのですから、
= 2.8 × 10-3
= 2.8 ミリ秒
かかります。したがって、選択肢イが正解です。
解答イ
【厳選問題 2 】
ターンアラウンドタイムの意味を知っていればわかります
一つのジョブについての,ターンアラウンドタイム,CPU 時間,入出力時間及び処理待ち時間の四つの時間の関係を表す式はどれか。ここで,ほかのオーバヘッド時間は考慮しないものとする。
ア 処理待ち時間 = CPU 時間 + ターンアラウンドタイム + 入出力時間
イ 処理待ち時間 = CPU 時間 – ターンアラウンドタイム + 入出力時間
ウ 処理待ち時間 = ターンアラウンドタイム – CPU 時間 – 入出力時間
エ 処理待ち時間 = 入出力時間 – CPU 時間 – ターンアラウンドタイム
選択肢に「処理待ち時間 = 」という式が並んでいますが、この問題のテーマは「処理待ち時間」ではありません。「ターンアラウンドタイムの意味を知っていますか?」 という問題です。
「ターンアラウンドタイム」は、「バッチ処理」の処理時間を示すものです。
バッチ( batch )は、「束」という意味であり、バッチ処理は「複数データをまとめて処理すること」を意味します。
たとえば、1 日の営業時間に発生した数多くのデータを、営業時間後にまとめて処理するのが、バッチ処理です。バッチ処理では、データの演算だけでなく、データの入出力にも多くの時間がかかります。
したがって、バッチ処理の処理時間であるターンアラウンドタイムは、
という式になります。
選択肢では、「データの演算時間」を「 CPU 時間」と示し、「データの入出力時間」を「入出力時間」と示しています。
さらに「処理待ち時間」という項目がありますが、これはバッチ処理にかかる時間なので、ターンアラウンドタイムに加えます。
以上のことから、
という式ができ、これを「処理待ち時間 = 」に変形すると、
になります。したがって、選択肢ウが正解です。
解答ウ
【厳選問題 3 】
落ち着いてやってみれば、とっても簡単な計算です
あるオンラインリアルタイムシステムでは,20 件/秒の頻度でトランザクションが発生する。このトランザクションは CPU 処理と 4 回の磁気ディスク入出力処理を経て終了する。磁気ディスク装置の入出力処理時間は 40 ミリ秒 / 回であり,CPU 処理時間は十分に短いものとする。それぞれの磁気ディスク装置が均等にアクセスされるとしたとき,このトランザクション処理には最低何台の磁気ディスク装置が必要か。
ア 3 イ 4 ウ 5 エ 6
一見して「うわっ! 難しそう」と思われる問題ですが、落ち着いてやってみれば、とっても簡単な問題です。こういう問題を練習しておくと、「やればできる!」という自信が付きます。
少しずつ問題の内容を見てみましょう。
あるオンラインリアルタイムシステムでは、20 件 / 秒の頻度でトランザクションが発生する
とは、単に「 1 秒間に 20 件の処理が発生する」と考えれば OK です。トランザクションは、処理のまとまりを意味する言葉であり、1 件、2 件と数えます。
このトランザクションは CPU 処理と 4 回の磁気ディスク入出力処理を経て終了する
とあり、さらに
磁気ディスク装置の入出力時間は 40 ミリ秒 / 回であり、CPU 時間は十分に短いものとする
なので、1 件のトランザクションの処理時間は、短い CPU 時間を無視して、4 回の磁気ディスク入出力処理だけの時間になります。
これは、4 回 × 40 ミリ秒 / 回 = 160 ミリ秒です。
それぞれの磁気ディスク装置が均等にアクセスされるとしたとき、このトランザクション処理には最低何台の磁気ディスク装置が必要か
ですから、1 秒間に 20 件のトランザクションを処理するために必要な磁気ディスク装置の台数を求めればよいのです。
1 件のトランザクションあたり 160 ミリ秒かかるので、1 台の磁気ディスク装置は、
= 1000 ミリ秒 ÷ 160 ミリ秒
= 6.25 件
のトランザクションを処理できます。0.25 という中途半端な処理はできないので、端数を切り捨てて 6 件です。
1 台で 6 件を処理できるので、20 件を処理するには、20 件 ÷ 6 件 = 3.33・・・台の磁気ディスク装置が必要であり、端数を切り上げて 4 台です。
したがって、選択肢イが正解です。どうです? とっても簡単な問題だったでしょう!
解答イ
【厳選問題 4 】
この問題で第3正規形かどうかを判断する方法を覚えよう
“発注伝票” 表を第3 正規形に書き換えたものはどれか。ここで、下線部は主キーを表す。
発注伝票 (注文番号, 商品番号, 商品名, 注文数量)
ア 発注 (注文番号, 注文数量) 商品 (商品番号, 商品名) イ 発注 (注文番号, 注文数量) 商品 (注文番号, 商品番号, 商品名) ウ 発注 (注文番号, 商品番号, 注文数量) 商品 (商品番号, 商品名) エ 発注 (注文番号, 商品番号, 注文数量) 商品 (商品番号, 商品名, 注文数量)
関係データベースの正規化理論がテーマの問題です。
正規化理論では、表の状態を「非正規形」「第 1 正規形」「第 2 正規形」「第 3 正規形」に区別し、それぞれ以下のように定義しています。
「繰り返し」「部分従属性」「推移従属性」が排除すべきものであり、すべてを排除した状態が第3正規形です。
- 非正規形
- 繰り返しがある。
- 第 1 正規形
- 繰り返しを排除している。
- 第 2 正規形
- 第 1 正規形を満たし、さらに部分従属性を排除している。
- 第 3 正規形
- 第 2 正規形を満たし、さらに推移従属性を排除している。
理論的に考えると難しいのですが、第 3 正規形とは、早い話が「主キーに従属した列だけの表」です。
主キーとは、レコード(行)を特定できるユニークな情報を持つ列です。
従属とは「列 A によって列 B が特定できる」ということです。
これを「 A → B 」のように矢印で示すとわかりやすいでしょう。
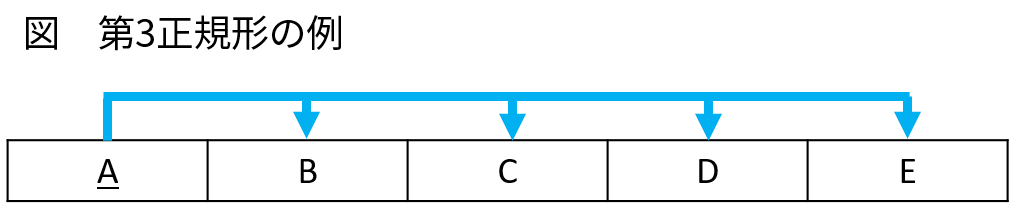
以下は、第 3 正規形の表の例です。A 、B 、C 、D 、E は、何らかの情報を持った列だとします。
主キーは、下線を付けた A です。主キー A から B 、C 、D 、E に向かって従属性の矢印が引けています。このような矢印だけが引ければ、第 3 正規形だと判断できます。
それでは、問題を見てみましょう。
問題では「表名( 列名1, 列名2, ・・・)」という形式で表を示していますが、わかりやすいように列を枠で囲んで表を示します。
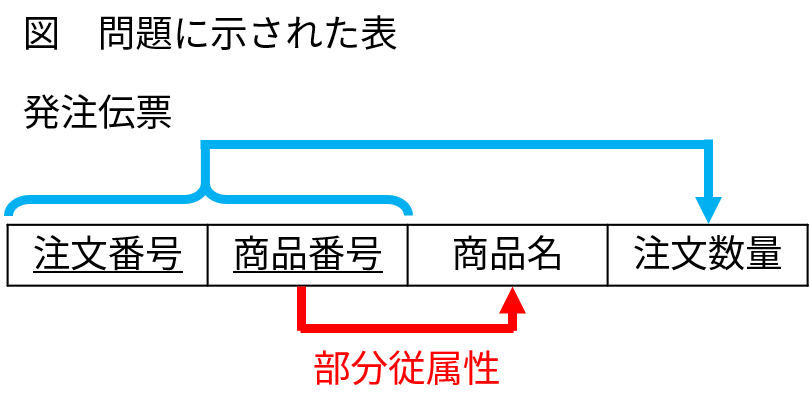
問題に示された「発注伝票」表は、「注文番号」と「商品番号」の 2 つの列をセットにして主キーにしています。このような主キーを「複合キー」と呼びます。
従属性の線を引くと、以下のように、「注文数量」は、複合キーの「注文番号」と「商品番号」に従属しますが、「商品名」は「商品番号」だけに依存します。
これを「部分従属性」と呼び、部分従属性の線があると第 3 正規形ではありません。第 3 正規形は、「主キーに従属した列だけの表」だからです。
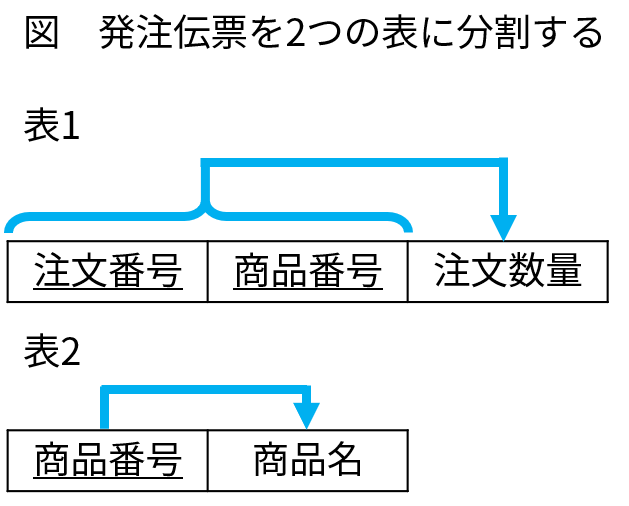
このような場合には、「注文番号」と「商品番号」の複合キーに従属する「注文数量」を持つ表 1 と、「商品番号」に従属する「商品名」を持つ表 2 に分割します。
したがって、選択肢ウが正解です。
解答ウ
searchタグで関連記事をチェック正規化
【厳選問題 5 】
M や N を使った式は、具体例を想定すればわかります
パスワードに使用できる文字の種類の数を M ,パスワードの文字数を n とするとき,設定できるパスワードの理論的な総数を求める数式はどれか。

M 種類の文字で文字数 n のパスワードを作ると、その総数はいくつになりますか? という問題です。
このように M だの n だのと言っている問題には、定番の解法があります。それは、「 M や n に具体的な数値を想定する」です。
選択肢があるのですから、その具体例を代入して同じ値になるものが正解です。
例として、M = 3 種類の文字「 A 」「 B 」「 C 」で、文字数 n = 2 のパスワードを作るとしましょう。
パスワードの総数は、
「 AA 」「 AB 」「 AC 」「 BA 」「 BB 」「 BC 」「 CA 」「 CB 」「 CC 」
の 9 通りです。
選択肢に示された式に、M = 3、n = 2 を代入すると、以下になります。
- 選択肢ア
- 32 = 9
- 選択肢イ
- ( 3 × 2 × 1 ) / ( 1 ) = 6
- 選択肢ウ
- ( 3 × 2 × 1 ) / ( ( 2 × 1 ) × ( 1 ) ) = 3
- 選択肢エ
- ( 4 × 3 × 2 × 1 ) / ( ( 2 × 1 ) × ( 2 × 1 ) ) = 6
9 になっている選択肢アが正解です。
解答ア
searchタグで関連記事をチェックテクニック 具体的な値を想定
記事をお読みいただきありがとうございます。
もしも、一度解いただけでは、よくわからない問題があったなら、わかるまで何度でも練習してください。「やるべき問題」は「わかるまでやるべき問題」だからです。
この厳選問題大全集が、受験者の皆様のお役に立てば幸いです。
label 関連タグ
免除試験を受けた 74.9% の方が、科目A免除資格を得ています。
※独習ゼミは、受験ナビ運営のSEプラスによる試験対策eラーニングです。

「厳選5題」過去問と解説|令和元年度 秋期 の過去問やるならこれをやれ
update
「厳選5題」過去問と解説|平成31年度 春期 の過去問やるならこれをやれ
update
「厳選5題」過去問と解説|平成21年度 秋期 の過去問やるならこれをやれ
update
「厳選5題」過去問と解説 | 平成22年度 春期 の過去問やるならこれをやれ
update
「厳選5題」過去問と解説 | 平成22年度 秋期 の過去問やるならこれをやれ
update
「厳選5題」過去問と解説 | 平成23年度 春期 の過去問やるならこれをやれ
update
「厳選5題」過去問と解説 | 平成23年度 秋期 の過去問やるならこれをやれ
update
「厳選5題」過去問と解説 | 平成24年度 春期 の過去問やるならこれをやれ
update
「厳選5題」過去問と解説 | 平成24年度 秋期 の過去問やるならこれをやれ
update
「厳選5題」過去問と解説 | 平成25年度 春期 の過去問やるならこれをやれ
update
『プログラムはなぜ動くのか』(日経BP)が大ベストセラー
IT技術を楽しく・分かりやすく教える“自称ソフトウェア芸人”
大手電気メーカーでPCの製造、ソフトハウスでプログラマを経験。独立後、現在はアプリケーションの開発と販売に従事。その傍ら、書籍・雑誌の執筆、またセミナー講師として活躍。軽快な口調で、知識0ベースのITエンジニアや一般書店フェアなどの一般的なPCユーザの講習ではダントツの評価。
お客様の満足を何よりも大切にし、わかりやすい、のせるのが上手い自称ソフトウェア芸人。
主な著作物
- 「プログラムはなぜ動くのか」(日経BP)
- 「コンピュータはなぜ動くのか」(日経BP)
- 「出るとこだけ! 基本情報技術者」 (翔泳社)
- 「ベテランが丁寧に教えてくれる ハードウェアの知識と実務」(翔泳社)
- 「ifとelseの思考術」(ソフトバンククリエイティブ) など多数










