基本情報でわかる 論理演算 「真理値表を書けば、半加算器と全加算器の仕組みがわかる」

error
この記事は基本情報技術者試験の旧制度( 2022 年以前)の記事ですが、試験対策ではなく、技術用語を理解する上では問題ないと考えています。
試験対策としてお読みになる場合は、現在の試験制度では出題されない午後問題を一部題材にしているので、ご注意ください。
この連載では、基本情報技術者試験によく出題されるテクノロジー関連の用語を、午前問題と午後問題のセットを使って解説します。
午前問題で用語の意味や概念を知り、午後問題で技術の活用方法を知ってください。それによって、単なる丸暗記では得られない明確さで、用語を理解できるようになります。
今回のテーマは、論理演算で加算を実現する 半加算器 と 全加算器 です。
論理演算で加算を実現する 半加算器 とは? 全加算器 とは?
コンピュータの内部では、 0 と 1 だけの 2 進数でデータが表現され、 AND, OR, NOT, XOR などの論理演算でデータが処理されています。コンピュータの外部からは、加減乗除の四則演算を行っているように見えても、内部では論理演算が行われているのです。
試験には、論理演算を使って加算を実現する 加算器 に関する問題が出ます。減算、乗算、除算の問題が出ないのは、加算ができれば、他の演算ができるからです。
- マイナスの数を加算すれば、減算になります
- プログラムを作って加算を繰り返せば、乗算になります
- プログラムを作って減算を繰り返し、引けた回数をカウントすれば、除算になります
加算器には、半加算器( half adder )と 全加算器( full adder )があります。
半加算器は、 1 桁の 2 進数を 2 つ加算します。
全加算器は、 1 桁の 2 進数を 3 つ加算します。
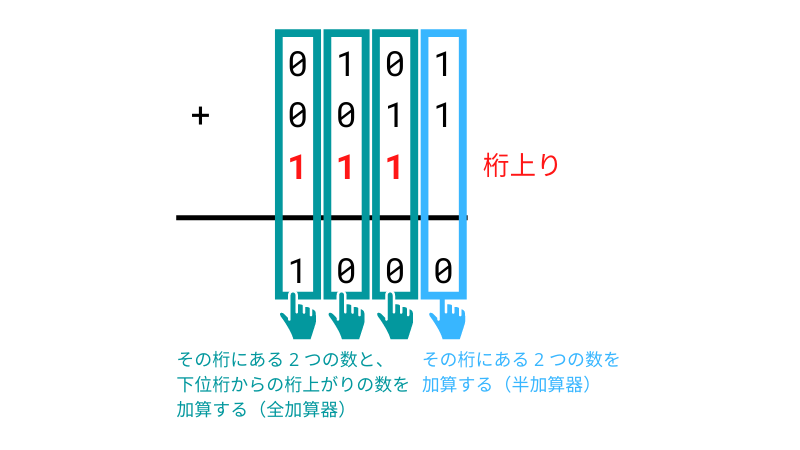
たとえば、 0101 と 0011 という 4 ビットの 2 進数を加算するとしましょう。
最下位ビットの加算では、その桁にある 2 つの数を加算するので、半加算器を使います。
それ以外の桁では、その桁にある 2 つの数と、下位桁からの桁上がりの数を加算するので、全加算器を使います。
したがって、 4 ビットの加算では、半加算器を 1 つと、全加算器を 3 つ使うことになります。
半加算器の仕組み
加算器の仕組みを説明しましょう。
まず、 1 桁の 2 進数を 2 つ加算する半加算器です。この加算のパターンには、以下に示した 4 通りがあります。
1 + 1 の結果が 1 0 の 2 桁になるので、他の結果も上位桁に 0 を置いて 2 桁に統一しています。「これらの結果を見て、論理演算で加算を実現する方法を見出してください」と言われても、すぐにはピンと来ないでしょう。
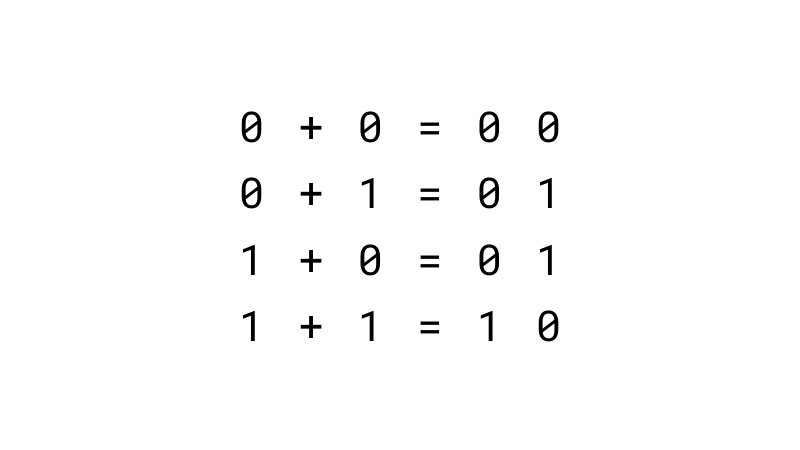
データに名前を付けて、真理値表を書いてみましょう。ここでは、加算する数を X および Y として、結果を C および S とします。
| X | Y | C | S |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
C は、 Carry (桁上がり)という意味で、 S は、 Sum (和)という意味です。この真理値表を見て、 X と Y にどのような論理演算を行うと、 C と S が得られるかを考えてください。
しばらく真理値表を見ていると「あっ、そうか!」と気付くはずです。
- C は、 X と Y の両方が 1 のときだけ 1 になります。これは、 X と Y の AND 演算です
- S は、 X と Y のどちらか一方だけが 1 のときだけ 1 になります。これは、 X と Y の XOR 演算です
| X | Y | C | S |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
以下は、半加算器の仕組みを示したものです。
図の左側から入力された X と Y の加算結果が、図の右側の S と C から出力されます。
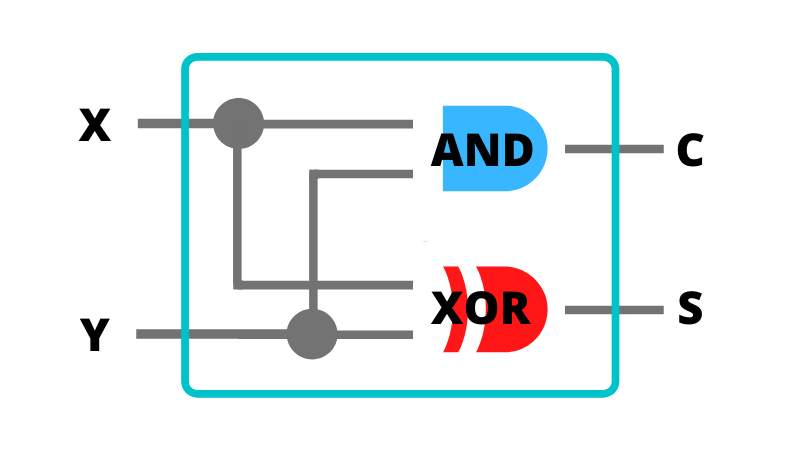
- 1 本の電線で、 1 桁の 2 進数が伝えられます
- 電線の交差に丸印がある部分は、つながっています
- 丸印がない部分は、立体交差であり、つながっていません
これは、回路図を書くときの決まり事です。
全加算器の仕組み
次は、 1 桁の 2 進数を 3 つ加算する半加算器の仕組みです。これは、「そもそも、なぜ半加算器や全加算器と呼ぶのか?」がわかれば、すんなり理解できるでしょう。
半加算器で 1 桁の 2 進数を 2 つ加算できるのですから、半加算器が 2 つあれば、 1 桁の 2 進数を 3 つ加算できます。つまり、半加算器を 2 つ使えば全加算器になるのです。逆に言えば、全加算器を半分にすれば、半加算器になります。だから「全」と「半」なのです。
以下は、全加算器の仕組みを示したものです。
図の左側から入力された X と Y と C´( C´ は、下位桁からの桁上がりを意味します)の加算結果が、図の右側の S と C から出力されます。
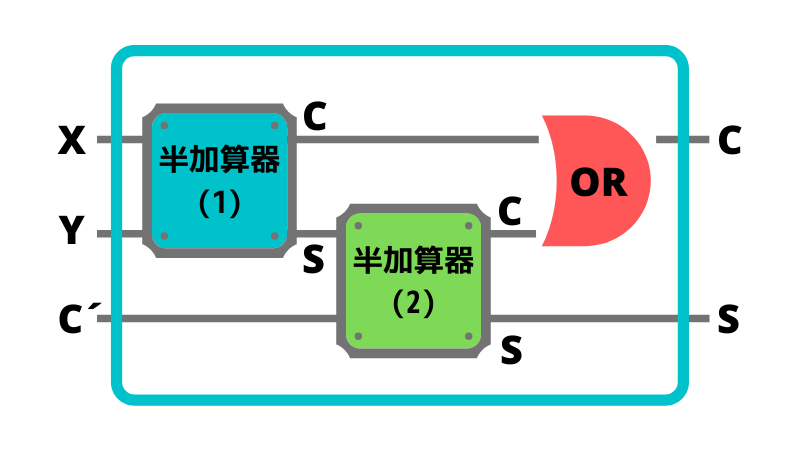
X と Y を半加算器 (1) で加算し、
その結果の S と C´ を半加算器 (2) で加算し、
その結果の S が、全加算器の S になります。
全加算器の C は、
半加算器 (1) の C と
半加算器 (2) の C を
OR 演算して得られます。
なぜなら、半加算器 (1) または半加算器 (2) のいずれかで桁上がりがあれば、それが全加算器の桁上がりになるからです。「または」は OR 演算です。
半加算器と全加算器に関する午前問題
半加算器と全加算器の仕組みがわかったところで、午前問題を解いてみましょう。以下は、半加算器に関する午前問題です。
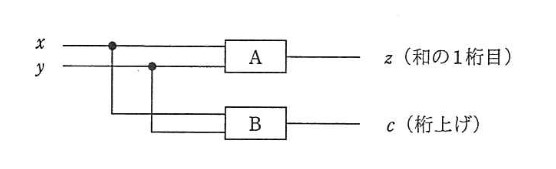
「 A 」の素子は、和を求めるので XOR 回路です。
「 B 」の素子は、桁上がりを求めるので AND 回路です。
選択肢では、論理演算の名前を日本語で示しています。 XOR は「排他的論理和」であり、 AND は「論理積」なので、選択肢アが正解です。
図に示す, 1 桁の 2 進数 x と y を加算して, z ( 和の 1 桁目 ) 及び c ( 桁上げ )を出力する半加算器において, A と B の素子の組合せとして,適切なものはどれか。
| A | B | |
|---|---|---|
| ア | 排他的論理和 | 論理積 |
| ィ | 否定論理積 | 否定論理和 |
| ウ | 否定論理和 | 排他的論理和 |
| エ | 論理積 | 論理和 |
解答ア
以下は、全加算器に関する午前問題です。全加算器が、 1 桁の 2 進数を 3 つ加算するものであることを知っていれば、簡単に問題を解けるでしょう。
ここでは、
y に 0 ,
z( z は、下位桁からの桁上がりだと思われます)に 1 を入力
するので、 1 と 0 と 1 が加算されて、 10 という結果が得られます。
結果の C が 1 で、 S が 0 なので、選択肢ウが正解です。
図は全加算器を表す論理回路である。図中の x に 1 , y に 0 , z に 1 を入力したとき,出力となる c (けた上げ数) ,s (和) の値はどれか。

| c | s | |
|---|---|---|
| ア | 0 | 0 |
| イ | 0 | 1 |
| ウ | 1 | 0 |
| エ | 1 | 1 |
解答ウ
半加算器と全加算器に関するに関する午後問題
今度は、午後問題を解いてみましょう。
以下の問題(問題の一部を抜粋しています)では、半加算器を 1 つと全加算器を 3 つ使った 4 ビットの加算器が示されています。
この加算器で、マイナスの数を加算するという内容です。つまり、加算器で減算を行うのです。
半加算器と全加算器に関する次の記述を読んで,設問 1 ~ 3 に答えよ。
(設問 1 と設問 2 を省略します)
- 設問 3
- A, B 及び S を 2 の補数表現による 4 ビットの符号付 2 進整数とし,それぞれのビット表現を A4A3A2A1, B4B3B2B1 及び S4S3S2S1で表す (符号ビットは A4, B4 及び S4 )。
- 図 3は, A と B の加算を行い,結果を S に求める加算器であり,半加算器と全加算器で実現されている。ここで,C1 C4 は半加算器及び全加算器からのけた上がりを表す。
- この加算器に,A として-1 を,Bとして -2 (いずれも 10 進表記) を与えたとき,図 3 の C1 〜 C4の値として正しい組合せを,解答群の中から選べ。

解答群
| C1 | C2 | C3 | C4 | |
|---|---|---|---|---|
| ア | 0 | 1 | 0 | 0 |
| イ | 0 | 1 | 0 | 1 |
| ウ | 0 | 1 | 1 | 0 |
| エ | 0 | 1 | 1 | 1 |
| オ | 1 | 0 | 0 | 0 |
| カ | 1 | 0 | 0 | 1 |
| キ | 1 | 0 | 1 | 0 |
| ク | 1 | 0 | 1 | 1 |
4 ビットの 2 の補数表現を使うと、
-1 は 1111 になり、
-2 は 1110 になります。
これを 4 ビットの加算器の A4A3A2A1 と B4B3B2B1 に入力すると、 1 つの半加算器と 3 つの全加算器の和( S1 ~ S4 )と桁上がり( C1 ~ C4 )は、以下のようになります。
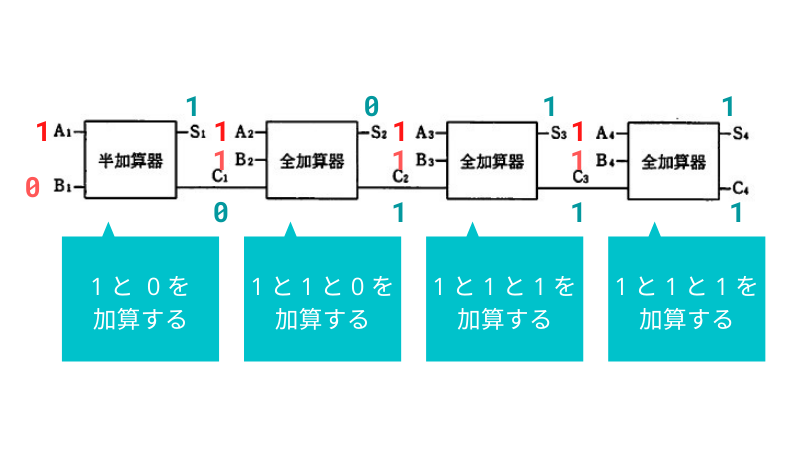
したがって、選択肢エが正解です。この加算器では、図の左側が下位桁であることに注意してください。
解答設問 3 エ
いかがでしたか?
論理演算を実現する半加算器と全加算器の仕組みを、しっかりと理解できたでしょう。
この連載では、今後も、多くの受験者が苦手としている用語を取り上げて行きます。それでは、またお会いしましょう!
label 関連タグ免除試験を受けた 74.9% の方が、科目A免除資格を得ています。
※独習ゼミは、受験ナビ運営のSEプラスによる試験対策eラーニングです。

基本情報でわかる IPアドレス と サブネットマスク
update
基本情報でわかる ホワイトボックステスト
update
基本情報でわかる トランザクション
update
基本情報でわかる コンパイラ 最適化
update
基本情報でわかる CRC 「具体例を見て体験すれば仕組みがわかる」
update
基本情報でわかる 浮動小数点 「3つの情報で1つの数を表す仕組みを知れば、浮動小数点数がわかる」
update
基本情報でわかる MIME タイプ 「電子メールの仕組みを知れば役割がわかる」
update
基本情報でわかる 7セグメントLED 「 1 と 0 を書き込めば点灯するパターンがわかる」
update
基本情報でわかる 論理演算 「真理値表を書けば、半加算器と全加算器の仕組みがわかる」
update
基本情報でわかる SMTP / POP3 「ITエンジニア視点で見れば役割がわかる」
update
『プログラムはなぜ動くのか』(日経BP)が大ベストセラー
IT技術を楽しく・分かりやすく教える“自称ソフトウェア芸人”
大手電気メーカーでPCの製造、ソフトハウスでプログラマを経験。独立後、現在はアプリケーションの開発と販売に従事。その傍ら、書籍・雑誌の執筆、またセミナー講師として活躍。軽快な口調で、知識0ベースのITエンジニアや一般書店フェアなどの一般的なPCユーザの講習ではダントツの評価。
お客様の満足を何よりも大切にし、わかりやすい、のせるのが上手い自称ソフトウェア芸人。
主な著作物
- 「プログラムはなぜ動くのか」(日経BP)
- 「コンピュータはなぜ動くのか」(日経BP)
- 「出るとこだけ! 基本情報技術者」 (翔泳社)
- 「ベテランが丁寧に教えてくれる ハードウェアの知識と実務」(翔泳社)
- 「ifとelseの思考術」(ソフトバンククリエイティブ) など多数









