今週の午後問題〔問題〕アルゴリズム ハフマン符号化を用いた文字列圧縮 2019 年度 春期
error
この記事は基本情報技術者試験の旧制度( 2022 年以前)の記事です。
この記事の題材となっている「午後問題」は現在の試験制度では出題されません。 ご注意くださいませ。
このコーナーでは毎週月曜に午後の必須選択問題から 1 問ピックアップして出題し、 解答欄 を設け、読者の皆さまも参加して解答できます! その週の金曜にはその解答と 矢沢久雄 さんによる 解説 ページを公開し、皆さんの正解率も発表します。
今週から「アルゴリズム」に絞って出題中です!今回は 「 2019 年度 春期 ハフマン符号化を用いた文字列圧縮」です。
ぜひ腕試しにお使い下さい!
今週の午後問題
2019 年度 春期 アルゴリズム ハフマン符号化を用いた文字列圧縮
問 1
ハフマン符号化を用いた文字列圧縮に関する次の記述を読んで,設問 1 ~ 3 に答えよ。
- 文字列中の文字の出現回数を求め,出現回数表を作成する。例えば,文字列 “AAAABBCDCDDACCAAAAA” (以下,文字列 α という)中の文字の出現回数表は,表 1 のとおりになる。
表 1 文字列 α 中の文字の出現回数表 文字 A B C D 出現回数 10 2 4 3 - 文字の出現回数表に基づいてハフマン木を作成する。
ハフマン木の定義は,次のとおりである。- 節と枝で構成する二分木である。
- 親である節は,子である節を常に二つもち,子の節の値の和を値としてもつ。
- 子をもたない節(以下,葉という)は文字に対応し,出現回数を値としてもつ。
- 親をもたない節(以下,根という)は,文字列の文字数を値としてもつ。
文字列 α に対応するハフマン木の例を,図 1 に示す。
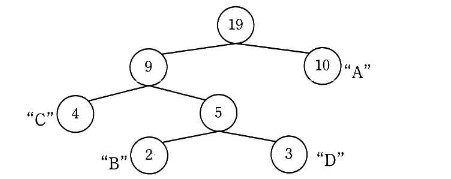
注記 丸の中の数値は各節がもつ値を表す。 “A” ~ “D” は葉に対応する文字を表す。
図 1 文字列 α に対応するハフマン木の例ハフマン木は,次の手順で配列によって実現する。
- 節の値を格納する 1 次元配列を用意する。
- 文字の出現回数表に基づいて,各文字に対応する葉の値を,配列の先頭の要素から順に格納する。
- 親が作成されていない節を二つ選択し,選択した順に左側の子,右側の子とする親の節を一つ作成する。この節の値を,配列中で値が格納されている最後の要素の次の要素に格納する。節の選択は節の値の小さい順に行い,同じ値をもつ節が二つ以上ある場合は,配列の先頭に近い要素に値が格納されている節を選択する。
- 親が作成されていない節が一つになるまで ⅲ を繰り返す。
- ハフマン木から文字のビット列(以下,ビット表現という)を次の手順で作成する。
- 親と左側の子をつなぐ枝に 0 ,右側の子をつなぐ枝に 1 の値をもつビットを割り当てる。
- 文字ごとに根から対応する葉までたどったとき,枝のビット値を順に左から並べたものを各文字のビット表現とする。
図 2 に示すとおり,根から矢印のようにたどると,文字列 α の文字 “B” のビット表現は 010 となる。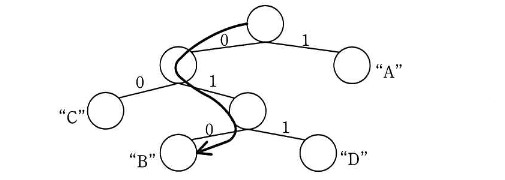
注記 線分は枝を表し,枝の上の数値は各枝のビット値を表す。
図 2 文字列 α における文字 “B” のビット表現の作成例
- 文字列の全ての文字を 3. で得られたビット表現に置き換えて,ビット列を作成する。
設問 1
次の記述中のに入れる正しい答えを,解答群の中から選べ。
圧縮率 =
ハフマン符号化によって圧縮したときの総ビット長
2 ビットの固定長で表現したときの総ビット長
a に関する解答群
| 文字 | A | B | C | D |
|---|---|---|---|---|
| ビット表現 | 010 | 1 | 00 | 011 |
| 文字 | A | B | C | D |
|---|---|---|---|---|
| ビット表現 | 010 | 0 | 01 | 111 |
| 文字 | A | B | C | D |
|---|---|---|---|---|
| ビット表現 | 100 | 0 | 101 | 11 |
| 文字 | A | B | C | D |
|---|---|---|---|---|
| ビット表現 | 100 | 1 | 00 | 01 |
b に関する解答群
ア 0.77 イ 0.85 ウ 0.88 エ 0.92
設問 2
ハフマン木を作成するプログラム 1 の説明及びプログラム 1 を読んで,プログラム 1 中のに入れる正しい答えを,解答群の中から選べ。
〔プログラム 1 の説明〕
- 四つの 1 次元配列
parent,left,right及びfreqの同じ要素番号に対応する要素の組み(以下,要素組という)によって,一つの節を表す。要素番号は 0 から始まる。四つの配列の大きさはいずれも十分に大きく,全ての要素は -1 で初期化されている。 - 図 3 に,図 1 に示したハフマン木を表現した場合の各配列の要素がもつ値を示す。配列
parentには親,配列leftには左側の子,配列rightには右側の子を表す要素組の要素番号がそれぞれ格納され,配列freqには節の値が格納される。節が葉のとき,配列leftと配列rightの要素の値は,いずれも -1 である。図 3 では,要素番号 0 ~ 3の要素組が,順に文字 “A” ~ “D” の葉に対応している。節が根のとき,配列parentの要素の値は -1 である。
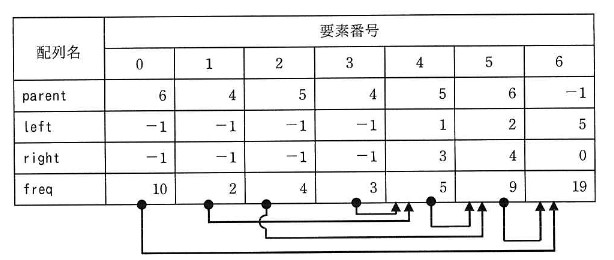
注記 矢印  は,始点,終点の二つの要素組に対応する節が子と親の関係にあることを示す。
は,始点,終点の二つの要素組に対応する節が子と親の関係にあることを示す。
図 3 図 1 に示したハフマン木を表現する四つの配列 - 副プログラム Huffman は,次の 1 ~ 5 を受け取り,ハフマン木を表現する配列を作成する。
- 葉である節の個数
size - 初期化された配列
parent - 初期化された配列
left - 初期化された配列
right - 初期化された後,文字の出現回数が要素番号 0 から順に格納された配列
freq
- 葉である節の個数
- 副プログラム SortNode は,親が作成されていない節を抽出し,節の値の昇順に整列し,節を表す要素組の要素番号を順に配列 node に格納し,その個数を変数 nsize に格納する。行番号 19 ~ 24 で親が作成されていない節を表す要素組の要素番号を抽出し,行番号 25 で節の値の昇順に整列する。
- 副プログラム Sort (プログラムは省略)は,節を表す要素組の要素番号の配列 node を受け取り,要素番号に対応する要素組が表す節の値が昇順となるように整列する。節の値が同じときの順序は並べ替える直前の順序に従う。
- 副プログラム Huffman,SortNode 及び Sort の引数の仕様を,表 2 ~ 4 に示す。
| 引数 | データ型 | 入出力 | 説明 |
|---|---|---|---|
size |
整数型 | 入力/出力 | 節の個数 |
parent[] |
整数型 | 入力/出力 | 節の親を表す要素組の要素番号を格納した配列 |
left[] |
整数型 | 入力/出力 | 節の左側の子を表す要素組の要素番号を格納した配列 |
right[] |
整数型 | 入力/出力 | 節の右側の子を表す要素組の要素番号を格納した配列 |
freq[] |
整数型 | 入力/出力 | 節の値を格納した配列 |
| 引数 | データ型 | 入出力 | 説明 |
|---|---|---|---|
size |
整数型 | 入力 | 節の個数 |
parent[] |
整数型 | 入力 | 節の親を表す要素組の要素番号を格納した配列 |
freq[] |
整数型 | 入力 | 節の値を格納した配列 |
nsize |
整数型 | 出力 | 配列 node 中の,整列対象とした節の個数 |
node[] |
整数型 | 出力 | 節の値の昇順に整列した,親が作成されていない節を表す要素組の要素番号を格納した配列 |
| 引数 | データ型 | 入出力 | 説明 |
|---|---|---|---|
freq[] |
整数型 | 入力 | 節の値を格納した配列 |
nsize |
整数型 | 入力 | 配列 node 中の,整列対象の節の個数 |
node[] |
整数型 | 入力/出力 | 節を表す要素組の要素番号を格納した配列 |
○副プログラム: Huffman(整数型: size, 整数型: parent[], 整数型: : left[], 整数型: right[], 整数型: freq[])
○整数型: i, j, nsize
○整数型: node[]
• SortNode(size, parent, freq, nsize, node)
■ "[ c ]"
| ・ i ← node[0] /* 最も小さい値をもつ要素組の要素番号 */
| ・ j ← node[1] /* 2 番目に小さい値をもつ要素組の要素番号 */
| ・ left[size] ← i
| ・ right[size] ← j
| ・ freq[size] ← freq[i] + freq[j] /* 子の値の合計 */
| ・ parent[i] ← size /* 子に親の節の要素番号を格納 */
| ・ parent[j] ← size /* 子に親の節の要素番号を格納 */
| ・ size + size + 1
| ・ SortNode(size, parent, freq, nsize, node)
■
○副プログラム: SortNode(整数型: size, 整数型: parent[], 整数型: freq[], 整数型: nsize, 整数型: node[])
○整数型: i
・ nsize ← 0
■ i: 0, i < size, 1
| ▲ "[ d ]"
| | ・ node[nsize] ← i
| | ・ nsize ← nsize + 1
| ▼
■
・ Sort(freq, nsize, node)c, d に関する解答群
ア nsize ≧ 0 イ nsize ≧ 1 ウ nsize ≧ 2
エ parent[i] < 0 オ parent[i] > 0 カ size ≦ nsize
キ size ≧ nsize設問 3
ハフマン木から文字のビット表現を作成して表示するプログラム 2 の説明及びプログラム 2 を読んで,プログラム 2 中のに入れる正しい答えを,解答群の中から選べ。
〔プログラム 2 の説明〕
- ビット表現を求めたい文字に対応する葉を表す要素組の要素番号を,副プログラム Encode の引数 k に与えて呼び出すと,ハフマン木から文字のビット表現を作成して表示する。
- 副プログラム Encode の引数の仕様を,表 5 に示す。
| 引数 | データ型 | 入出力 | 説明 |
|---|---|---|---|
| k | 整数型 | 入力 | 節を表す要素組の要素番号 |
| parent[] | 整数型 | 入力 | 節の親を表す要素組の要素番号を格納した配列 |
| left[] | 整数型 | 入力 | 節の左側の子を表す要素組の要素番号を格納した配列 |
- 副プログラム Encode は,行番号 2 の条件が成り立つとき,副プログラム Encode を再帰的に呼び出す。これによって,ハフマン木を葉から根までたどっていく。
- 根にたどり着くと次は葉に向かってたどっていく。現在の節が親の左側の子のときは 0 を,右側の子のときは 1 を表示する。
- 関数 print は,引数で与えられた文字列を表示する。
○副プログラム: Encode(整数型:k, 整数型: parent[], 整数型: left[])
▲ "[ e ]"
| ・ Encode(parent[k], parent, left)
| ▲ "[ f ]"
| | ・ print("0") /* 0 を表示する */
|-+---
| | ・ print("1") /* 1 を表示する */
| ▼
▼ e に関する解答群
ア k ≧ 0 イ left[k] = -1 ウ left[k] ≧ 0
エ parent[k] = -1 オ parent[k] ≧ 0f に関する解答群
ア left[k] = k イ left[parent[k]] = k
ウ parent[k] = k エ parent[left[k]] = k問題のヒント
この問題のテーマとなっているハフマン符号は、情報の基礎理論の分野で、基本情報技術者試験のシラバス(出題内容の細目を示した資料)に示されています。問題を解く前提知識として、ハフマン符号の仕組みと作り方を知っておきましょう。
ハフマン符号化は、文字列の中で使われている個々の文字の出現回数を求め、出現頻度が多いほど短いビット数で符号化します。これによって、すべての文字を同じビット数で符号化することに比べて、文字列全体のサイズを小さくできます。
ハフマン符号は、ハフマン木を使って作ります。出現頻度が少ない順に文字をつないだ二分木を作り、木の根から目的の文字までたどるときに、
左に行くときに 0 を
右に行くときに 1 を
割り当てるのです。
これによって、出現頻度が少ない文字ほど長いビット数で符号化されます。逆に言えば、出現頻度が多い文字ほど短いビット数で符号化されるのです。
以上の前提知識を持って、問題に取り組んでください。
みんなの解答欄
こちらから解答できます!
今週の金曜に解答解説ページを、ご解答頂いた方の正解率とともに公開します !!
label 関連タグ
免除試験を受けた 74.9% の方が、科目A免除資格を得ています。
※独習ゼミは、受験ナビ運営のSEプラスによる試験対策eラーニングです。

今週の午後問題〔解答〕アルゴリズム 文字列の誤りの検出 2017 年度 秋期
update
今週の午後問題〔問題〕アルゴリズム 文字列の誤りの検出 2017 年度 秋期
update
今週の午後問題〔解答〕アルゴリズム ヒープの性質を利用したデータの整列 2018 年度 春期
update
今週の午後問題〔問題〕アルゴリズム ヒープの性質を利用したデータの整列 2018 年度 春期
update
今週の午後問題〔解答〕アルゴリズム 整数式の解析と計算 2018 年度 秋期
update
今週の午後問題〔問題〕アルゴリズム 整数式の解析と計算 2018 年度 秋期
update
今週の午後問題〔解答〕アルゴリズム ハフマン符号化を用いた文字列圧縮 2019 年度 春期
update
今週の午後問題〔問題〕アルゴリズム ハフマン符号化を用いた文字列圧縮 2019 年度 春期
update
今週の午後問題〔解答〕情報セキュリティ SSH による通信 2017 年度 秋期
update
今週の午後問題〔問題〕情報セキュリティ SSH による通信 2017 年度 秋期
update- 基本情報技術者試験 の受験勉強をレポート頂ける方を募集中です!
- ツイッター で過去問を配信しています
姉妹サイト 「IT資格の歩き方」 では応用情報技術者以上の情報処理技術者試験の対策記事があります!
基本情報技術者試験を合格されたら、「IT資格の歩き方」で末永く、スキルアップにお役立てください!











