今週の午後問題〔問題〕アルゴリズム ヒープの性質を利用したデータの整列 2018 年度 春期

error
この記事は基本情報技術者試験の旧制度( 2022 年以前)の記事です。
この記事の題材となっている「午後問題」は現在の試験制度では出題されません。 ご注意くださいませ。
このコーナーでは毎週月曜に午後の必須選択問題から 1 問ピックアップして出題し、 解答欄 を設け、読者の皆さまも参加して解答できます! その週の金曜にはその解答と 矢沢久雄 さんによる 解説 ページを公開し、皆さんの正解率も発表します。
今週から「アルゴリズム」に絞って出題中です!今回は 「 2018 年度 春期 ヒープの性質を利用したデータの整列」です。
ぜひ腕試しにお使い下さい!
今週の午後問題
2018 年度 春期 アルゴリズム ヒープの性質を利用したデータの整列
問 1
次のプログラムの説明及びプログラムを読んで,設問 1 , 2 に答えよ。
〔プログラム 1 の説明〕
- 配列の要素番号は, 0 から始まる。
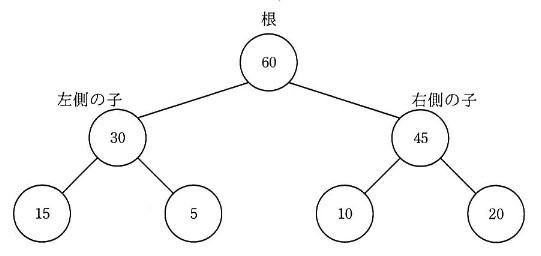
- 副プログラム makeHeap は,整数型の 1 次元配列 data に格納されている hnum 個 (hnum > 0) のデータを,次の 01 ~ 03 の規則で整数型の 1 次元配列 heap に格納して,ヒープを配列で実現する。この状態を, “配列 heap は,ヒープの性質を満たしている” という。
- 配列要素 heap[i] (i = 0,1,2,…) は,節に対応する。配列要素 heap[i] には,節が保持する値を格納する。
- 配列要素 heap[0] は,根に対応する。
- 配列要素 heap[i] (i = 0,1,2,…) に対応する節の左側の子は配列要素 heap[2 × i + 1] に対応し,右側の子は配列要素 heap[2 × i + 2] に対応する。子が一つの場合,左側の子として扱う。
- 図 1 のヒープの例に対応した配列 heap の内容を,図 2 に示す。
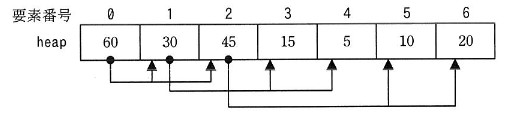
注記 印 → は,始点,終点の二つの配列要素に対応する節が,親子関係にあることを表す。
図 2 図 1 のヒープの例に対応した配列 heap の内容 - 親の要素番号と子の要素番号を関係付ける三つの関数がある。
-
- 整数型: lchild(整数型: i )
- 要素番号 i の配列要素に対応する節の左側の子の配列要素の要素番号 2 × i + 1 を計算して返却する。
-
- 整数型: rchild(整数型: i )
- 要素番号 i の配列要素に対応する節の右側の子の配列要素の要素番号 2 × i + 2 を計算して返却する。
-
- 整数型: parent(整数型: i )
- 要素番号 i の配列要素に対応する節の親の配列要素の要素番号 (i – 1) = 2 (小数点以下切捨て) を計算して返却する。
-
- 副プログラム swap は,二つの配列要素に格納されている値を交換する。
- 副プログラム makeHeap の引数の仕様を表 1 に,副プログラム swap の引数の仕様を表 2 に示す。
| 引数 | データ型 | 入出力 | 説明 |
|---|---|---|---|
| data[] | 整数型 | 入力 | データが格納されている 1 次元配列 |
| heap[] | 整数型 | 出力 | ヒープの性質を満たすようにデータを格納する 1 次元配列 |
| hnum | 整数型 | 入力 | データの個数 |
| 引数 | データ型 | 入出力 | 説明 |
|---|---|---|---|
| heap[] | 整数型 | 入力/出力 | 交換対象のデータが格納されている 1 次元配列 |
| i | 整数型 | 入力 | 交換対象の要素番号 |
| j | 整数型 | 入力 | 交換対象の要素番号 |
○副プログラム: makeHeap( 整数型: data[], 整数型: heap[], 整数型: hnum )
○整数型: i, k
■ i : 0, i < hnum, 1
| ・ heap[i] ← data[i] /* heap にデータを追加 */
| ・ k ← i
| ■ k > 0
| | ▲ "[ a ]"
| | | ・ swap(heap, k, "[ b ]")
| | | ・ k ← parent(k)
| | +---
| | | ・ break /* 内側の繰返し処理から抜ける */
| | ▼
| ■
■
○副プログラム: swap( 整数型: heap[], 整数型: i, 整数型: j )
○整数型: tmp
・ tmp ← heap[i]
・ heap[i] ← heap[j]
・ heap[j] ← tmp設問 1
プログラム 1 中のに入れる正しい答えを,解答群の中から選べ。
a に関する解答群
ア heap[k] > heap[lchild(k)]
イ heap[k] > heap[parent(k)]
ウ heap[k] > heap[rchild(k)]
エ heap[k] < heap[lchild(k)]
オ heap[k] < heap[parent(k)]
カ heap[k] < heap[rchild(k)]
b に関する解答群
ア heap[hnum – 1]
イ heap[k]
ウ parent(hnum – 1)
エ parent(k)
設問 2
〔プログラム 2 の動作〕の記述中のに入れる正しい答えを,解答群の中から選べ。
〔プログラム 2 の説明〕
- 副プログラム heapSort は,最初に副プログラム makeHeap を使って,配列 heap にデータを格納する。配列 heap は,整列対象領域と整列済みデータ領域に分かれている (図 3 参照)。 last は,整列対象領域の最後の配列要素の要素番号を示している。最初は,配列 heap 全体が整列対象領域であり,このとき last の値は hnum – 1 である。
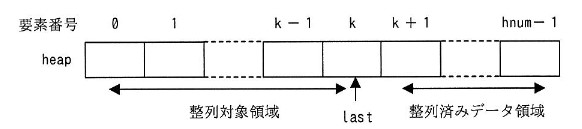
図 3 配列 heap における整列対象領域と整列済みデータ領域 - 整列対象領域がヒープの性質を満たすとき,配列要素 heap[0] の値は,この領域での最大の値となっている。そこで,配列要素 heap[0] の値と配列要素 heap[last] の値を交換し, last の値を 1 減らして,整列対象領域の範囲を狭め,整列済みデータ領域を広げる。値の交換によって,整列対象領域はヒープの性質を満たさなくなるので,副プログラム downHeap を使って,整列対象領域のデータがヒープの性質を満たすように再構成する。これを繰り返すことによって,整列済みデータ領域には昇順に整列されたデータが格納されることになる。
- 副プログラム heapSort の引数の仕様を表 3 に,副プログラム heapSort で使用する副プログラム downHeap の引数の仕様を表 4 に示す。
| 引数 | データ型 | 入出力 | 説明 |
|---|---|---|---|
| data[] | 整数型 | 入力 | 整列対象のデータが格納されている 1 次元配列 |
| heap[] | 整数型 | 出力 | 整列済みのデータを格納する 1 次元配列 |
| hnum | 整数型 | 入力 | データの個数 |
| 引数 | データ型 | 入出力 | 説明 |
|---|---|---|---|
| heap[] | 整数型 | 入力/出力 | 整列対象のデータを格納する 1 次元配列 |
| hlast | 整数型 | 入力 | 整列対象領域の最後の要素番号 |
(行番号)
○副プログラム: heapSort( 整数型: data[], 整数型: heap[], 整数型: hnum )
○整数型: last
・ makeHeap(data, heap, hnum)
■ last: hnum - 1, last > 0, -1
| ・ swap(heap, 0, last) /* heap[0] と heap[last] の値を交換 */
| ・ downHeap(heap, last - 1) /* heap を再構成 */
■fast_rewindfast_rewindfast_rewindα(行番号)
○副プログラム: downHeap( 整数型: heap[], 整数型: hlast )
○整数型 : n, tmp
・ n ← 0
■ lchild(n) ≦ hlast
| ・ tmp ← lchild(n)
| ▲ rchild(n) ≦ hlast
| | ▲ heap[tmp] ≦ heap[rchild(n)]
| | | ・ tmp ← rchild(n)
| | ▼
| ▼
| ▲ heap[tmp] > heap[n]
| | ・ swap (heap, n, tmp)
| +---
| | ・ return /* downHeap から抜ける */
| ▼
| ・ n ← tmp
■〔プログラム 2 の動作〕
副プログラム heapSort の行番号 5 の副プログラム swap の実行が終了した直後の 配列要素 heap[0] の値は,cとなる。このため,配列 heap の要素番号 0 から hnum – 2 までのデータは,根に対応する配列要素 heap[0] が最大の値をもつというヒープの性質を満たさなくなる。
副プログラム heapSort の行番号 6 で呼び出している副プログラム downHeap は,配列 heap の整列対象領域の要素番号 0 から hlast までのデータがヒープの性質を満たすように,その領域のデータを次の手順で再構成する。
- 配列要素の値の大きさを比較する際に使用する要素番号を n とし, n の初期値を 0 とする。
- 要素番号 n の配列要素に対応する節の左側の子の要素番号を tmp に代入する。要素番号 n の子が二つあり (rchild(n) ≦ hlast) ,右側の子の値が左側の子の値d,右側の子の要素番号を tmp に代入する。
- 子に対応する配列要素 heap[tmp] の値と,その親に対応する配列要素 heap[n] の値とを比較し,配列要素 heap[tmp] の値が大きければ,配列要素 heap[n] の値と配列要素 heap[tmp] の値を交換し, tmp を次の n として 2. に戻る。ここで,副プログラム downHeap の行番号 15 において最初に n に代入する tmp の値は,eである。
c に関する解答群
ア 5 イ 10 ウ 15 エ 20
d に関する解答群
ア 以下のときには イ 以上のときには
ウ よりも大きいときには エ よりも小さいときには
e に関する解答群
ア 1 イ 2 ウ 3
エ 4 オ 5 カ 6
問題のヒント
ヒープというデータ構造を使った、ヒープソートがテーマです。ヒープもヒープソートも、基本情報技術者試験のシラバス(出題内容の細目を示した資料)に示されているので、あらかじめ知っておくべきことです。
ヒープ( heap )は、「堆積物」という意味であり、一般的に上(親)にあるデータが下(子)にあるデータより小さくなるように配置しますが、この問題では、逆になっていることに注意してください。これは、ヒープから取り出したデータを格納する手順の都合です。
堆積物という意味であっても、プログラムにおけるヒープは、二分木として表現されます。二分木では、 1 つの要素が 2 つの要素につながります。つながりの情報は、連結リストのポインタで示すこともできますが、この問題では、ヒープを表す配列に要素を格納する際のルールによって、二分木の親と子のつながりを示しています。
問題にヒープの例が示されているので、それを想定して手順の説明とプログラムを読むとわかりやすいでしょう。
みんなの解答欄
こちらから解答できます!
今週の金曜に解答解説ページを、ご解答頂いた方の正解率とともに公開します !!
label 関連タグ
免除試験を受けた 74.9% の方が、科目A免除資格を得ています。
※独習ゼミは、受験ナビ運営のSEプラスによる試験対策eラーニングです。

今週の午後問題〔解答〕アルゴリズム 文字列の誤りの検出 2017 年度 秋期
update
今週の午後問題〔問題〕アルゴリズム 文字列の誤りの検出 2017 年度 秋期
update
今週の午後問題〔解答〕アルゴリズム ヒープの性質を利用したデータの整列 2018 年度 春期
update
今週の午後問題〔問題〕アルゴリズム ヒープの性質を利用したデータの整列 2018 年度 春期
update
今週の午後問題〔解答〕アルゴリズム 整数式の解析と計算 2018 年度 秋期
update
今週の午後問題〔問題〕アルゴリズム 整数式の解析と計算 2018 年度 秋期
update
今週の午後問題〔解答〕アルゴリズム ハフマン符号化を用いた文字列圧縮 2019 年度 春期
update
今週の午後問題〔問題〕アルゴリズム ハフマン符号化を用いた文字列圧縮 2019 年度 春期
update
今週の午後問題〔解答〕情報セキュリティ SSH による通信 2017 年度 秋期
update
今週の午後問題〔問題〕情報セキュリティ SSH による通信 2017 年度 秋期
update- 基本情報技術者試験 の受験勉強をレポート頂ける方を募集中です!
- ツイッター で過去問を配信しています
姉妹サイト 「IT資格の歩き方」 では応用情報技術者以上の情報処理技術者試験の対策記事があります!
基本情報技術者試験を合格されたら、「IT資格の歩き方」で末永く、スキルアップにお役立てください!










