論理演算｜やさしい基礎理論
2024-04-17 更新
この連載は、基本情報技術者試験の受験者を対象としたものです。
多くの受験者が苦手としている「情報の基礎理論」の分野から毎回1つずつテーマをあげて、やさしくポイント解説と問題解説を行います。
苦手分野を克服して、試験の得点をアップしましょう。
今回のテーマは、論理演算です。
論理演算の種類
「論理演算」は、命題を対象とした演算です。命題とは、真か偽かを判断できる文や式のことです。
たとえば、「5は3より大きい（真と判断できる）」や「3は5より大きい（偽と判断できる）」などが命題です。
よく使われる論理演算の種類は、以下4つです。
「and（論理積）」・「or（論理和）」・「not（否定）」・「xor（排他的論理和、エックスオア）」
これらの論理演算で、真と偽を演算して、演算結果も真か偽になります。真と偽のことを「真理値」と呼びます。
論理演算の意味は、英語の意味と同じです。
andは「かつ」、orは「または」、notは「～でない」、xor（exclusive or）は「排他的にまたは」という意味です。
A and Bの演算結果
「AかつB」という意味なので、AとBの両方が真のときに真となり、その他の場合は偽になります。
A or Bの演算結果
「AまたはB」という意味なので、AとBのいずれかが真のときに（両方が真でもよい）真となり、その他の場合は偽になります。
not Aの演算結果
「Aでない」という意味なので、Aが真なら偽になり、Aが偽なら真になります。
A xor Bの演算結果
「A 排他的にまたは B」という意味なので、AとBの一方だけが真のときに真となり、その他の場合は偽になります。どちらか一方だけが真であることを「排他的（他を排除する）」と呼んでいるのです。
A and BやA or Bのように、論理演算を使った式を論理式と呼びます。
以下に論理式で、and、or、not、xorの演算結果を示したものを記載します。
ここでは、AやBという変数ではなく、真および偽という値で、論理式と演算結果を示しています。
（1）and（論理積、かつ）
偽 and 偽 ＝ 偽
偽 and 真 ＝ 偽
真 and 偽 ＝ 偽
真 and 真 ＝ 真
（2）or（論理和、または）
偽 or 偽 ＝ 偽
偽 or 真 ＝ 真
真 or 偽 ＝ 真
真 or 真 ＝ 真
（3）not（否定、～でない）
not 偽 ＝ 真
not 真 ＝ 偽
（4）xor（排他的論理和、排他的にまたは）
偽 xor 偽 ＝ 偽
偽 xor 真 ＝ 真
真 xor 偽 ＝ 真
真 xor 真 ＝ 偽
論理演算は、プログラムの分岐処理やデータベースの検索などで、いくつかの条件（条件は命題の一種です）を結び付けたり、条件を否定したりするときに使われます。
真と偽の真理値を1と0の数値に対応させると、論理演算は2進数の演算であるとみなせます。
たとえば、真 and 真 ＝ 真は、1 and 1 ＝ 1という2進数の演算とみなせます。
コンピュータの内部では、電気信号で表された2進数を演算する仕組みとして、論理演算が使われています。
ド・モルガンの法則
ド・モルガンの法則は、論理式を変形する法則です。
以下にド・モルガンの法則を示します。
法則（1） : not (A and B) ＝ not A or not B
「A and Bの結果をnotした論理式は、not Aとnot Bをorした論理式と等しい（論理式を変形できる）」
法則（2） : not (A or B) ＝ not A and not B
「A or Bの結果をnotした論理式は、not Aとnot Bをandした論理式と等しい（変形できる）」
ド・モルガンの法則は、人間の感覚として、すんなり理解できます。
例として、法則に示された論理式のAを「美味しい」、Bを「安い」として、and、or、notを「かつ」「または」「～でない」に置き換えてみましょう。
法則の（1）は「（美味しい、かつ、安い）でない ＝ 美味しくない、または、安くない」です。
法則の（2）は「（美味しい、または、安い）でない ＝ 美味しくない、かつ、安くない」です。
どちらも、人間の感覚として、すんなり理解できるでしょう。
論理演算に関する問題の例（その1）
論理演算に関する問題を2つ紹介しましょう。
はじめは、論理式の真理値から命題の真理値を求める問題です。
問1（出典：H31春問3）
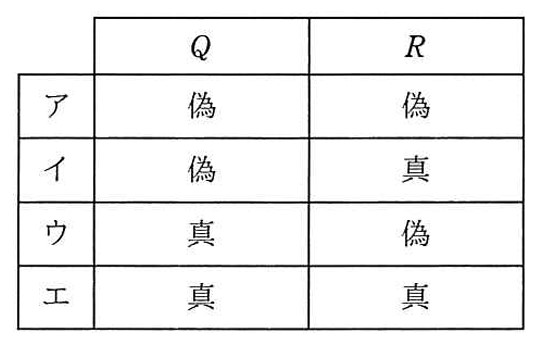
Ｐ、Ｑ、Ｒはいずれも命題である。命題Ｐの真理値は真であり、命題 (not Ｐ) or Ｑ及び命題 (not Ｑ) or Ｒのいずれの真理値も真であることが分かっている。Ｑ、Ｒの真理値はどれか。ここで、Ｘ or ＹはＸとＹの論理和、not ＸはＸの否定を表す。
＜解説＞
一見して難しそうな問題に思えるかもしれませんが、論理演算の意味を知っていれば簡単に解けますので、落ち着いて順番に論理式を見ていきましょう。
まず、P ＝ 真なので、not P ＝ 偽です。
次に、not P or Q ＝ 偽 or Q ＝ 真なので、Q ＝ 真です。
次に、Q ＝ 真とわかったので、not Q ＝ 偽です。
次に、not Q or R ＝ 偽 or R ＝ 真なので、R ＝ 真です。
以上のことから、PとQは、どちらも真であり、選択肢エが正解です。
論理演算に関する問題の例（その2）
次は、論理式を変形する問題です。
ド・モルガンの法則を使うことで、問題に示された複雑な論理式をシンプルな論理式に変形できます。
この問題では、and、or、notを・、＋、－（上付きのバー）で示しています。
問2（出典：H21春問3）
＜解説＞
問題に示された論理式を、and、or、notを使った表記にすると、not ((not A or B)and(A or not C))になります。
これを見て「andの演算結果がnot演算されているので、ド・モルガンの法則を使って式を変形できる」と気付いてください。
下記に、式を変形する手順の例を示します。
ド・モルガンの法則を使って式を変形する手順の例
（1）not ((not A or B) and (A or not C)) ・・・not (□ and △)の形式である。
（2）not (not A or B) or not (A or not C) ・・・not □ or not △に変形する。
（3）not not A and not B or not (A or not C)) ・・・式の前側をnot □ and not △に変形する。
（4）A and not B or not (A or not C) ・・・not not A＝AなのでAに変形する。
（5）A and not B or not A and not not C ・・・式の後側をnot □ and not △に変形する。
（6）A and not B or not A and C ・・・not not C＝CなのでCに変形する。
A and not B or not A and Cに変形できたので、選択肢アが正解です。
基本情報技術者試験の公開問題を見ると、過去に出題された問題の再利用が多いことがわかります。
したがって、試験に合格するために最も効率的で効果的な学習方法は、できなかった問題があれば、できるようになるまで練習することです。
もしも、今回取り上げた問題がすぐにできなかったら、できるようになるまで練習してください。
それでは、またお会いしましょう！
label 関連タグ免除試験を受けた 74.9% の方が、科目A免除資格を得ています。
※独習ゼミは、受験ナビ運営のSEプラスによる試験対策eラーニングです。
『プログラムはなぜ動くのか』（日経BP）が大ベストセラー
IT技術を楽しく・分かりやすく教える“自称ソフトウェア芸人”
大手電気メーカーでＰＣの製造、ソフトハウスでプログラマを経験。独立後、現在はアプリケーションの開発と販売に従事。その傍ら、書籍・雑誌の執筆、またセミナー講師として活躍。軽快な口調で、知識０ベースのＩＴエンジニアや一般書店フェアなどの一般的なＰＣユーザの講習ではダントツの評価。
お客様の満足を何よりも大切にし、わかりやすい、のせるのが上手い自称ソフトウェア芸人。
主な著作物
- 「プログラムはなぜ動くのか」（日経BP）
- 「コンピュータはなぜ動くのか」（日経BP）
- 「出るとこだけ! 基本情報技術者」 (翔泳社)
- 「ベテランが丁寧に教えてくれる ハードウェアの知識と実務」（翔泳社）
- 「ｉｆとｅｌｓｅの思考術」（ソフトバンククリエイティブ） など多数
play_circle_filledYouTube でも学べる
人気記事
稼働率の計算方法がわかる｜かんたん計算問題
update 2021-02-09
基本情報技術者試験 とは ～難易度や過去問、勉強法、勉強計画など疑問に答えます
update 2023-03-29
やるべき or やる必要がない過去問の見分け方「厳選5題」過去問と解説シリーズ
update 2021-12-21
略語でわかる MIPS の計算方法｜かんたん計算問題
update 2022-10-31
基本情報でわかる 浮動小数点 「3つの情報で1つの数を表す仕組みを知れば、浮動小数点数がわかる」
update 2021-12-03
基本情報でわかる FIFO LFU LRU 「略語の意味がわかればわかる」
update 2021-12-02
過去問の解き方知りたいぜ | よく出る「鉄板問題」を解説
update 2020-03-23
基本情報でわかる 論理演算 「真理値表を書けば、半加算器と全加算器の仕組みがわかる」
update 2021-12-16
基本情報技術者試験のシラバス改定｜Ver9.0の概要
update 2024-02-07
工数の計算方法がわかる｜かんたん計算問題
update 2021-02-09