情報の符号化|やさしい基礎理論

この連載は、基本情報技術者試験の受験者を対象としたものです。
多くの受験者が苦手としている「情報の基礎理論」の分野から毎回1つずつテーマをあげて、やさしくポイント解説と問題解説を行います。苦手分野を克服して、試験の得点をアップしましょう。
今回のテーマは、 情報の符号化 です。
ビット数と表せる情報の個数
コンピュータの内部では、あらゆる情報を数値で取り扱っています。そのため、文字や画像など本来数値ではない情報を取り扱うには、それらを数値で表す必要があります。 本来数値ではない情報を数値で表したもの を「 符号(コード) 」と呼び、 情報を数値に置き換えること を「 符号化 」と呼びます。
コンピュータの内部では、0と1だけで数値を表す2進数が使われています。2進数のビット数(桁数)によって、表せる情報の個数が決まります。1ビットで表せる情報は、0と1の2個です。
「ONとOFF」や「YesとNo」という情報であれば、1ビットで符号化できます。たとえば「ON=1、OFF=0」や「Yes=1、No=0」とします。2ビットで表せる情報は、00、01、10、11の4個です。「春夏秋冬」や「東西南北」という情報であれば、2ビットで符号化できます。たとえば「春=00、夏=01、秋=10、冬=11」や「東=00、西=01、南=10、北=11」とします。
表1に1~8ビットで表せる数値の範囲と情報の個数を示します。
表1 1~8ビットで表せる数値の範囲と情報の個数
| ビット数 | 数値の範囲 | 情報の個数 |
|---|---|---|
| 1 | 0~1 | 2 |
| 2 | 00~11 | 4 |
| 3 | 000~111 | 8 |
| 4 | 0000~1111 | 16 |
| 5 | 00000~11111 | 32 |
| 6 | 000000~111111 | 64 |
| 7 | 0000000~1111111 | 128 |
| 8 | 00000000~11111111 | 256 |
1ビット増えるごとに、表せる情報の個数は2倍になります。
1ビットなら2個、2ビットなら2×2=4個、3ビットなら2×2×2=8個、・・・、8ビットなら2×2×2×2×2×2×2×2=256個です。
nビットなら2をn回掛けるので2のn乗個です。
固定長符号と可変長符号
符号には、「 固定長符号 」と「 可変長符号 」があります。
固定長符号は、すべての情報を同じビット数で符号化したものです。
可変長符号は、情報によってビット数を変えたものです。
取り扱いが簡単なので、多くの場合に、固定長符号が使われますが、可変長符号を使うと、数多くの情報を格納したファイルや通信データの全体のサイズを小さくできる、というメリットがあります。
可変長符号では、連続して並べられた情報から個々の符号を区切れるように符号化しなければなりません。
たとえば、極端な例ですが「1111111111111111」という連続して並べられた情報があるとしましょう。これが8ビットの固定長符号なら、8ビットごとに「11111111」「11111111」と区切って2つの情報だとわかりますが、1、11、111、1111という可変長符号を並べたものなら、どこで区切ればよいのかがわかりません。個々の符号を区切れる可変長符号の具体例は、後で示す「情報の符号化に関する問題の例(その2)」で紹介します。
情報の符号化に関する問題の例(その1)
情報の符号化に関する問題を2つ紹介しましょう。
はじめは、ビット数が増えるとビットパターンの個数(表せる情報の個数)が何倍になるかという問題です。
問題1 (出典:H28秋問4)
32ビットで表現できるビットパターンの個数は、24ビットで表現できる個数の何倍か。
ア:8
イ:16
ウ:128
エ:256
<解説>
1ビット増えるごとに、表せる情報の個数は2倍になります。32ビットは、24ビットより32-24=8ビット多いので、表せる情報の個数は2×2×2×2×2×2×2×2=256倍です。したがって、選択肢エが正解です。
情報の符号化に関する問題の例(その2)
次は、可変長符号であるハフマン符号の問題です。
ハフマンは、この符号化の考案者(David Albert Huffman)の名前です。
問題2(出典:H30秋問4)
出現頻度の異なるA,B,C,D,Eの5文字で構成される通信データを,ハフマン符号化を使って圧縮するために,符号表を作成した。aに入る符号として,適切なものはどれか。

ア:001
イ:010
ウ:101
エ:110
<解説>
「ハフマン符号」は、出現頻度の多い情報ほど少ないビット数で符号化する(逆に言えば、出現頻度の少ない情報ほど多いビット数で符号化する)ことで、ファイルや通信データの全体のサイズを小さくします。
この問題では、A、B、C、D、Eの5つの文字(情報)があり、それを固定長符号で符号化すると、A=000、B=001、C=010、D=011、E=100のように、すべて3ビットになります。仮に、データ全体で100文字あるとすれば、そのサイズは3ビット×100文字=300ビットです。
これを、問題に示された可変長のハフマン符号で符号化すると、A=00(2ビット)、B=10(2ビット)、C=(2ビット)、D=[ a ](後で答えを示しますが3ビットです)、E=111(3ビット)です。仮に、データ全体に100文字あるとすれば、A、B、C、D、Eの出現頻度が、26%、25%、24%、13%、12%なので、それぞれ26文字、25文字、24文字、13文字、12文字です。データ全体のサイズは、26文字×2ビット+25文字×2ビット+24文字×2ビット+13文字×3ビット+12文字×3ビット=225ビットです。固定長符号の300ビットと比べて、データ全体のサイズが小さくなりました。
ハフマン符号は、「ハフマン木」を使って作ります。この問題のハフマン木を図1に示します。
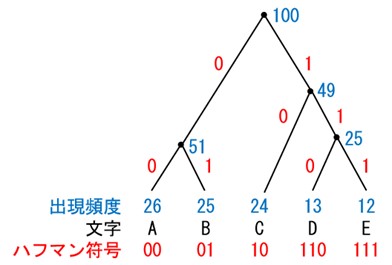
ハフマン木は、以下の手順で作成します。
(1)出現頻度の多い順に、出現頻度と情報(ここでは文字)を横方向に並べる。
(2)出現頻度の少ない順に2つを選んで枝(直線)で結び、その節(枝の結合部)に、2つの出現頻度を足した値を書き添える。
(3)木の枝が1つの根(木の最上部の結合部)にまとめられるまで、(2)を繰り返す。
(4)根から個々の情報までたどる枝の左側に0を、右側に1を書き添える。
(5)根から個々の情報までたどり、その際に通過した枝の0または1を上位桁から並べたものがハフマン符号になるので、それを個々の情報の下に書き添える。
出現頻度の多い情報ほど、木の根からその情報にたどりつくまでの枝の数が少なくなるので、符号のビット数が少なくなります。逆に、出現頻度の少ない情報ほど、木の根からその情報にたどりつくまでの枝の数が多くなるので、符号のビット数が多くなります。
Dのハフマン符号は、ハフマン木を根からDまでたどると1→1→0なので、110です。
したがって、この問題の正解は、選択肢エです。
ハフマン木で作られたハフマン符号は、連続して並べた情報から個々の符号を区切れます。ハフマン木で、根からそれぞれの情報にたどりつくまでの道筋は1つだけなので、連続して並べても区別できる符号になるからです。
たとえば、101110011001は、先頭から順に図1のハフマン符号に割り当てていくと、「10」「111」「00」「110」「01」に区切れるので、C、E、A、D、Bだとわかります。
* * *
基本情報技術者試験の公開問題を見ると、過去問題(過去の試験に出題された問題)の再利用が多いことがわかります。
したがって、試験に合格するために最も効率的で効果的な学習方法は、過去問題を数多く解き、できなかった問題があれば、できるようになるまで練習することです。もしも、今回取り上げた問題がすぐにできなかったら、できるようになるまで練習してください。
それでは、またお会いしましょう!
label 関連タグ免除試験を受けた 74.9% の方が、科目A免除資格を得ています。
※独習ゼミは、受験ナビ運営のSEプラスによる試験対策eラーニングです。

『プログラムはなぜ動くのか』(日経BP)が大ベストセラー
IT技術を楽しく・分かりやすく教える“自称ソフトウェア芸人”
大手電気メーカーでPCの製造、ソフトハウスでプログラマを経験。独立後、現在はアプリケーションの開発と販売に従事。その傍ら、書籍・雑誌の執筆、またセミナー講師として活躍。軽快な口調で、知識0ベースのITエンジニアや一般書店フェアなどの一般的なPCユーザの講習ではダントツの評価。
お客様の満足を何よりも大切にし、わかりやすい、のせるのが上手い自称ソフトウェア芸人。
主な著作物
- 「プログラムはなぜ動くのか」(日経BP)
- 「コンピュータはなぜ動くのか」(日経BP)
- 「出るとこだけ! 基本情報技術者」 (翔泳社)
- 「ベテランが丁寧に教えてくれる ハードウェアの知識と実務」(翔泳社)
- 「ifとelseの思考術」(ソフトバンククリエイティブ) など多数




















