今週の午後問題〔問題〕アルゴリズム 整数式の解析と計算 2018 年度 秋期

error
この記事は基本情報技術者試験の旧制度( 2022 年以前)の記事です。
この記事の題材となっている「午後問題」は現在の試験制度では出題されません。 ご注意くださいませ。
このコーナーでは毎週月曜に午後の必須選択問題から 1 問ピックアップして出題し、 解答欄 を設け、読者の皆さまも参加して解答できます! その週の金曜にはその解答と 矢沢久雄 さんによる 解説 ページを公開し、皆さんの正解率も発表します。
今週から「アルゴリズム」に絞って出題中です!今回は 「 2018 年度 秋期 整数式の解析と計算」です。
ぜひ腕試しにお使い下さい!
今週の午後問題
2018 年度 秋期 アルゴリズム 整数式の解析と計算
問 1
次のプログラムの説明及びプログラムを読んで,設問 1 ~ 3 に答えよ。
例 1: 2 × (34 – (5 + 67) ÷ 8)
〔プログラム 1 の説明〕
- 整数式は,文字の列で与えられる。整数式は,次のもので構成される。
- 符号のない数字 0 ~ 9 の並び
- 演算子 : +,-,×,÷
- 括弧: (,)
- 引数 Expression[] で整数式を,引数 ExpLen で整数式の文字数を,それぞれ受け取る。
- プログラム中の破線で囲んだ解析処理の部分では,受け取った整数式を解析し,計算に必要な情報を配列及び変数に設定する。
- プログラム中の破線で囲んだ計算処理の部分では, 3. で設定した情報を用いて,整数式の値を計算する。整数式の値は, Value[0] に得られる。
- 各配列の添字は, 0 から始まる。各配列の要素数は,十分に大きいものとする。
- 受け取った整数式に誤りはないものとする。また,計算の過程で,あふれやゼロ除算は発生しないものとする。
○整数型関数 : Compute(文字型: Expression[], 整数型: ExpLen) ○文字型: Operator[100] ○整数型: OpCnt, Priority[100], Value[100] ○文字型: chr ○整数型: i, ip, nest 解析処理(詳細は〔プログラム(解析処理の部分)〕に示す) 計算処理(詳細は〔プログラム(計算処理の部分)〕に示す) ・ return Value[0]
〔プログラム (解析処理の部分) の説明〕
- Expression[] で渡された整数式を解析し,計算に必要な情報を配列 Operator[],Priority[],Value[] 及び変数 OpCnt に設定する。関数 int() は,引数の数字が表す値を整数型で返す。
- 例 1 の整数式について,プログラム(解析処理の部分)を実行した直後の各配列及び変数の状態を,図 1 に示す。
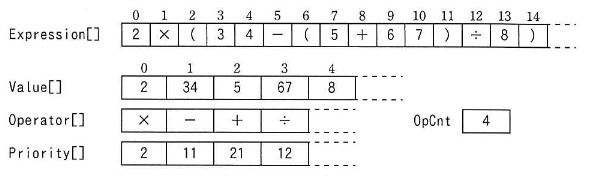
図 1 プログラム (解析処理の部分) を実行した直後の状態
・ OpCnt ← 0
・ Value[0] ← 0
・ nest ← 0
■ i: 0, i < ExpLen, 1
| ・ chr + Expression[i]
| ▲ ('0' ≦ chr) and (chr ≦ '9') /* 数字 0 ~ 9 か? */
| | ・ Value[OpCnt] ← 10 x Value[OpCnt] + int(chr)
| ▼
| ▲ (chr = '+') or (chr = '-') or (chr = 'x') or (chr = '÷')
| | ・ Operator [OpCnt] ← chr
| | ▲ (chr = '+') or (chr = '-')
| | | ・ Priority[OpCnt] ← nest + 1
| |-+-----
| | | ・ Priority[OpCnt] ← nest + 2
| | ▼
| | ・ OpCnt ← OpCnt + 1
| | ・ Value[OpCnt] ← 0
| ▼
| ▲ chr = '('
| | ・ nest ← nest + 10
| ▼
| ▲ chr = ')'
| | ・ nest ← nest – 10
| ▼
■
〔プログラム (計算処理の部分) の説明〕
- 整数式の値を計算していく。図 1 に示す各配列及び変数の状態から,プログラム (計算処理の部分) の最外側の繰返しを 1 回実行した直後の各配列及び変数の状態を,図 2 に示す。
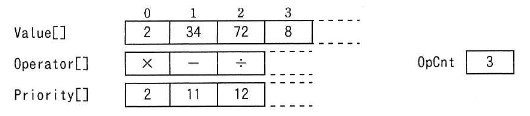
図 2 プログラム (計算処理の部分) の最外側の繰返しを 1 回実行した直後の状態
■ OpCnt > 0 | ・ ip ← 0 | ■ i: 1, i < OpCnt, 1 | | ▲ Priority[ip] < Priority[i] | | | ・ ip ← i | | ▼ | ■ | ・ chr ← Operator[ip] | ▲ chr = '+' | | ・ Value[ip] ← Value[ip] + Value[ip + 1] | ▼ | ▲ chr = '-' | | ・ Value[ip] ← Value[ip] - Value[ip + 1] | ▼ | ▲ chr = 'x' | | ・ Value[ip] ← Value[ip] x Value[ip + 1] | ▼ | ▲ chr = '÷' | | ・ Value[ip] ← Value[ip] ÷ Value[ip + 1] | ▼ | ■ i: ip + 1, i < OpCnt, 1 | | ・ Value[i] ← Value[i + 1] | | ・ Operator[i - 1] ← Operator[i] | | ・ Priority[i - 1] ← Priority[i] | ■ | ・ OpCnt ← OpCnt - 1 ■
設問 1
プログラム (解析処理の部分) に関する次の記述中のに入れる正しい答えを,解答群の中から選べ。
まず,行 3 及び 4 の処理では,定数として 10 を用いているが,この定数は 10 である必要はない。このプログラムにおいては,定数がaであれば常に正しい演算順序が保証される。
また,行 1 及び 2 の処理では,定数として 1 及び 2 を用いているが,次に示すように書き換えることが可能である。ここで,priLow 及び priHigh は整数の定数を表し,その値は priLow < priHigh とする。
1arrow_forward ・ Priority[OpCnt] ← nest + priLow 2arrow_forward ・ Priority[OpCnt] ← nest + priHigh
このように表現したとき,行 3 及び 4 の処理では, nest の値を増減する定数がbのときに限り正しい演算順序が保証されることになる。
a に関する解答群
ア 1 以上 イ 2 以上
ウ 11 以下 エ 12 以下
b に関する解答群
ア priHigh 以上 イ priHigh + 1 以上
ウ priHigh – priLow 以上 エ priHigh – priLow + 1 以上
設問 2
優先順位の等しい演算子が複数個含まれている整数式の,演算の実行順序について考察する。プログラムに関する次の記述中のに入れる正しい答えを,解答群の中から選べ。ここで, c1 ~ c3 に入れる答えは, c に関する解答群の中から組合せとして正しいものを選ぶものとする。
演算の実行順序によって,計算結果が異なることがある。例えば,次の四つの整数式のケースを考える。
ケース 2 : (12 + 3 + 1) ÷ 4 ÷ 2
ケース 3 : (12 – 3 – 1) × 4 × 2
ケース 4 : (12 – 3 – 1) ÷ 4 ÷ 2
これらのケースのうち,演算を左から実行しても右から実行しても,プログラムによる計算結果が等しくなるのは,ケースdである。
c に関する解答群
| c1 | c2 | c3 | |
|---|---|---|---|
| ア | 5 | ip ← 0 | ip ← OpCnt – 1 |
| イ | 6 | i : 1, i < OpCnt, 1 | i: OpCnt, i > 0, -1 |
| ウ | 6 | i : 1, i < Opcnt, 1 | i: OpCnt – 1, i > 0, -1 |
| エ | 7 | Priority[ip] < Priority[i] | Priority[ip] ≦ Priority[i] |
d に関する解答群
ア 1 イ 1 及び 2
ウ 1 及び 3 エ 1 及び 4
設問 3
プログラムの動作に関する次の記述中のに入れる正しい答えを,解答群の中から選べ。
例 3: +2 × (-3 + (-4))
符号付き整定数を含む整数式 2 × (-1)についてプログラム (解析処理の部分) を実行した結果を,図 3 に示す。
このように,符号付き整定数を含む整数式を受け取ったとき,プログラムはe。
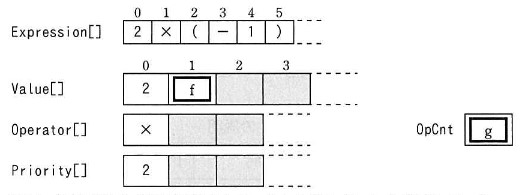
図 3 整数式 2 × (-1) についてプログラム (解析処理の部分) を実行した結果
e に関する解答群
- ア
- 整数式が符号付き整定数で始まる場合に、正しい値を返さない
- イ
- 整数式中に符号 – の付いた符号付き整定数がある場合に,正しい値を返さない
- ウ
- 整数式中に二つ以上の符号付き整定数が含まれる場合に,正しい値を返さない
- 工
- 正しい値を返す
f, g に関する解答群
ア -1 イ 0 ウ 1 エ 2
問題のヒント
2 × (34 – (5 + 67) ÷ 8) のような整数式を受け取って、その値を返すプログラムです。このテーマを聞いて「逆ポーランド記法」を思い浮かべるかもしれませんが、それとはまったく異なる手順が使われています。
手順は、詳しく示されています。プログラムは、一切穴埋めがなく、完成した状態になっています。プログラムの中に、 1 、 2 、 3 、・・・ という番号が付けられ、それぞれの部分で「どのようなデータなら正しい演算順序になるか」という設問になっています。
つまり、このプログラムは、あらゆる整数式の値を正しく求められるものではないのです。出題者が示した手順を読み取り、出題者の「こうしたらどうなる?」という設問に答える、という問題です。
その際に、ポイントになるのは、カッコや演算子の優先順位の判断です。
みんなの解答欄
こちらから解答できます!
今週の金曜に解答解説ページを、ご解答頂いた方の正解率とともに公開します !!
label 関連タグ
免除試験を受けた 74.9% の方が、科目A免除資格を得ています。
※独習ゼミは、受験ナビ運営のSEプラスによる試験対策eラーニングです。

今週の午後問題〔解答〕アルゴリズム 文字列の誤りの検出 2017 年度 秋期
update
今週の午後問題〔問題〕アルゴリズム 文字列の誤りの検出 2017 年度 秋期
update
今週の午後問題〔解答〕アルゴリズム ヒープの性質を利用したデータの整列 2018 年度 春期
update
今週の午後問題〔問題〕アルゴリズム ヒープの性質を利用したデータの整列 2018 年度 春期
update
今週の午後問題〔解答〕アルゴリズム 整数式の解析と計算 2018 年度 秋期
update
今週の午後問題〔問題〕アルゴリズム 整数式の解析と計算 2018 年度 秋期
update
今週の午後問題〔解答〕アルゴリズム ハフマン符号化を用いた文字列圧縮 2019 年度 春期
update
今週の午後問題〔問題〕アルゴリズム ハフマン符号化を用いた文字列圧縮 2019 年度 春期
update
今週の午後問題〔解答〕情報セキュリティ SSH による通信 2017 年度 秋期
update
今週の午後問題〔問題〕情報セキュリティ SSH による通信 2017 年度 秋期
update- 基本情報技術者試験 の受験勉強をレポート頂ける方を募集中です!
- ツイッター で過去問を配信しています
姉妹サイト 「IT資格の歩き方」 では応用情報技術者以上の情報処理技術者試験の対策記事があります!
基本情報技術者試験を合格されたら、「IT資格の歩き方」で末永く、スキルアップにお役立てください!










