午後問題の歩き方 | CASLⅡで必要となる2進数に関する知識
error
この記事は基本情報技術者試験の旧制度( 2022 年以前)の記事です。
この記事の題材となっている「午後問題」は現在の試験制度では出題されません。 ご注意くださいませ。
前回の記事 では、
- 「 CASLⅡの言語構文を覚えるだけなら、それほど時間はかかりません(簡単です)」
- 「ただし、問題を解くには、2 進数に関する様々な知識が必要 とされます(それほど簡単ではありません)」
ということを説明しました。
今回は、過去問題に出題されたプログラムを例にして、どのような知識が、どのような場面で必要とされるのか を説明します。
CASLⅡを選ぼうかどうか迷っている人の参考になれば幸いです。
-
error編集部注
- 本記事ではわかりやすいよう、プログラムの問題に背景を入れています。
もくじ
シフトと加算で乗算を行う手順を知っていますか?
平成 21 年度 春期 午後 問 12 のテーマは「 32 ビットの乗算」です。
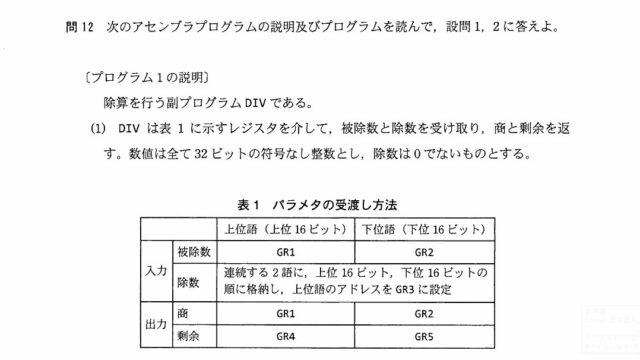
次のアセンブラプログラムの説明及びプログラムを読んで,設問 1 ,2 に答えよ。
【プログラムの説明】
32 ビットの乗算を行う副プログラム MULS である。
⁝
この問題を解くには、シフトと加算で 2 進数の乗算を行う手順を知っていなければなりません。
以下にシンプルな例題を示したので、手作業でやってみてください。演算結果は、初期状態でゼロクリアされているとします。
00000000000000000000000000001111 被乗数 × 00000000000000000000000000000101 乗数 ------------------------------------ 00000000000000000000000000000000 演算結果
まず、乗数 の 最下位桁 が 1 なら 演算結果 に 被乗数 を 加算 します。
次に、乗数 を 1 ビット論理右シフト して、次にチェックする桁を 最下位桁 に移動します。
そして、次の 加算 に合わせて、被乗数 を 1 ビット論理左シフト します。
これを、乗数 が 0 になるまで繰り返します。
00000000000000000000000000001111 被乗数 × 00000000000000000000000000000101 乗数 ------------------------------------ 00000000000000000000000000001111 + 00000000000000000000000000111100 ------------------------------------ 00000000000000000000000001001011 演算結果
この手順は、平成 21 年度 春期 だけでなく、何度も出題されています。
最下位桁が 1 かどうかチェックする方法がわかりますか?
先ほどの問題を解くための知識の説明を続けます。シフト と 加算 で 乗算 を行う手順の中で、乗数 の 最下位桁 が 1 かどうかをチェックします。
以下は、問題に示されたプログラムの一部です。
LP SRL GR2,1 ; 乗数を 1 ビット右にシフト
a
JZE FIN
JUMP NEXT ; 加算処理をスキップ
ADD32 ADDL GR6,GR4 ; 32 ビット + 32 ビット → 32 ビット
ADDL GR7,GRS
GR2 に格納されている 乗数を 1 ビット論理右シフトした後で、空欄 a には 最下位桁 が 1 なら ADD32 というラベルにジャンプする処理が入ります。
選択肢から答えを選ぶには、最下位桁 が 1 であることを判断する方法を知っていなければなりません。
ア JMI ADD32 イ JMI LP
ウ JOV ADD32 エ JOV LP
オ JPL ADD32 カ JPL LP
答えは、選択肢ウ の JOV ADD32 です。
最下位桁 が 1 なら、論理右シフト によって、その 1 がはみ出します。それを JOV( Jump OVerflow, オーバーフローならジャンプする)で判断するのです。
一般的な感覚では、上位桁 からはみ出すことが オーバーフロー(桁あふれ)ですが、コンピュータでは、下位桁 からはみ出すこともオーバーフロー なのです。
なお、別の年度の問題では、論理右シフト することではなく、「 #0001 と AND 演算した結果が ゼロ でないなら 最下位桁 が 1 である」と判断するプログラムが出題されたこともあります。
いろいろな方法があるので、 1 つに決め付けないようにしましょう。
ビット演算で数値を数字に変換する方法がわかりますか?
次の例は、平成 25 年度 秋期 午後 問 12「数字列の時間と数値の秒との変換」 です。
この問題を解くには、ビット演算で 1 桁の数値を数字に変換する 方法を知っていなければなりません。
プログラムの中で、該当する部分を以下に示します。たったの 1 行だけです。空欄 c の選択肢には、レジスタ の名前が示されています。
レジスタの名前を選ぶには、この処理を見て「 1 桁 の数値を 数字に変換する処理 だ!」 とピンと来なければなりません。
18 | OR c ,='0'
以下は、試験問題に添付されている文字の符号表です。
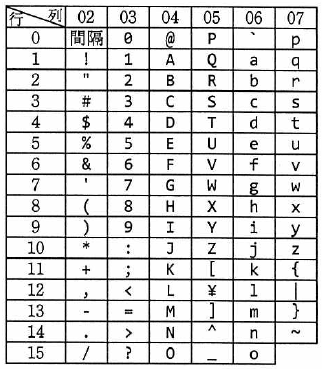
‘0’ ~ ‘9’ という数字(文字)には、#30 ~ #39(先頭の # は、16 進数であることを意味します)という符号が割り当てられています。
したがって、たとえば GR0 に 0 ~ 9 の数値が格納されていれば、それと #30 を OR 演算することで、#30 ~ #39 という数字に変換できます。
#30 は、 ‘0’ の文字コードなので、このプログラムでは、
OR GR0,=#30
という処理を、
OR GR0,='0'
と表記しています。
「 ‘0’ の文字コードと OR 演算しているんだから、何をやっているかわかるよね!」というヒントなのでしょう(たぶん)。
このような知識は、1 つひとつ確実に覚えていきましょう。そうすれば、他の問題で応用ができます。
たとえば、以下は平成 30 年度 春期 午後 問 12「数字列の数値への変換」に出題されたプログラムの一部です。
先ほど覚えた知識があれば、これを見て、すぐに何をしているのかピンと来たでしょう。
SUBL GR4,='0' ; 1 桁を数値に変換ご丁寧にコメントも付けられていますが、この処理は、GR4 に格納されている 数字 を 数値 に 変換 しています。
たとえば、GR4 に ‘5’ という数字の符号の #35 が格納されているとすれば、そこから ‘0’ の符号の #30 を引くことで、数値の 5 に変換できます。
この変換は、
AND GR4,#000F
と ビット演算 でもできますが、SUBL という 減算 を使っているのは、出題者の好みなのでしょう。
#FFFF が 2 進数でいくつか、すぐにわかりますか?
ビット演算 を行うには、 マスク を作る必要があります。
マスクとは、たとえば、0101010101010101 の下位 8 ビットを取り出すときには、
0101010101010101
AND 0000000011111111
という ビット演算 を行いますが、このときの 0000000011111111 というパターンのことです。
以下は、平成 29 年度 秋期 午後 問 12「ビット列の検索・置換」 に出題されたプログラムの一部です。
「マスク作成」というコメントにあるように、GR6 に マスク を作成しています。
仮に、GR3 の値が 10 進数 で 8 だとしたら、GR6 には、どのようなパターンのマスクが作られるでしょう。トレースしてみてください。
LD GR6,=#FFFF ; マスク作成
SRL GR6,0,GR3
XOR GR6,=#FFFF
マスクのパターンを見出すには、#FFFF という 16 進数が、2 進数で 1111111111111111 であることを知っておくべきです。
- 4 行目で GR6 に 1111111111111111 が格納される
- 5 行目で GR6 が 8 ビット右論理シフト されて 0000000011111111 になる
- 6 行目で GR6 の 0000000011111111 と 1111111111111111 が XOR 演算される
- GR6 は 1111111100000000 になる
この時点の GR6 の内容が マスク です。
6 行目にも知っておくべき知識があります。
CASLⅡ の論理演算の命令は、AND 演算、OR 演算、XOR 演算だけであり、データを反転する NOT 演算がありません。
NOT 演算を行いたい場合は、すべての桁 が 1 の マスク と XOR 演算することで代用します。
すべての桁 が 1 のデータは、16 進数で #FFFF です。6 行目の
XOR GR6,=#FFFF を見て 「これはデータの反転だ!」とわかるようになりましょう。
#FFFF が 2 の補数表現 でマイナス 1 だとすぐにわかりますか?
最後に、もう一度だけ、目的を実現する方法を 1 つに決め付けないようにしましょう、ということを言っておきたいので、以下のプログラムを見てください。
これは、平成 23 年度 秋期 午後 問 12「除算と2 進 10 進数文字列変換」 に出題されたプログラムの一部です。
注目してほしいのは、「商の初期化」 とコメントされた部分にある #FFFF です。
DIV START ; 減算を用いた 32 ビット除算
PUSH 0,GR6
PUSH 0,GR7
LD GR6,GR1
LD GR7,GR2
LD GR1,=#FFFF ; 商の初期化
LD GR2,=#FFFF
LP LD GR4,GR6
LD GR5,GR7
ADDL GR2,=1 ; 商のカウントアップ
先ほども説明したように、#FFFF という 16 進数は、 2 進数 で 1111111111111111 です。
それでは、この 1111111111111111 は、マスク を作るためのデータなのでしょうか。
ここでは、違います。
1111111111111111 は、2 の補数表現 の -1 です。
すべての桁が 1 の 2 進数を見て「 2 の補数表現 で -1 だ」とわかるようになってください。
それを 16 進数で示した #FFFF を見ても「これは -1 だ」とわかるようになりましょう。
これも、知っておくべき重要な知識です。
この問題では、引き算 を繰り返して、被除数 から 除数 を引けた回数を 商(除算の結果)とします。
それなら、「商の初期化」とコメントされた部分では、商を格納するレジスタをゼロクリアするべきです。
ところが、このプログラムでは、繰り返し処理の先頭(「商のカウントアップ」とコメントされた部分)で、引き算を行う前に、商をカウントアップしています。ここで -1 が ゼロになる のでつじつまが合うのです。
ちょっと、わかりにくいですね。
そもそも、CASLⅡ では、= の後に 10 進数を記述することもできるので、商を -1 で 初期化 するなら、= #FFFF ではなく、= -1 と表記すべきです(これは、筆者の個人的な意見です)。
ここも、わかりにくいですね。
でも、そういう問題が出題されているのですから、あれこれ文句を言わずに、とにかく練習あるのみです。
実際の試験に出題された 2 進数の知識を見て、どう思いましたか?
「これなら、できそうだ!」と思った人は、迷わず CASLⅡ を選んでください。本試験に向けて、CASLⅡの過去問題をドンドン練習してください。
それとは逆に「こりゃ、だめだ!」と思った人は、本試験まで時間がなければ、CASLⅡをキッパリと断念して、別の言語を選びましょう。
次回は、表計算の学習手順と、問題を解くために必要とされる知識を説明しますので、参考にしてください。
それでは、またお会いしましょう!
labelそのほかのプログラミング言語の記事
label 関連タグ
免除試験を受けた 74.9% の方が、科目A免除資格を得ています。
※独習ゼミは、受験ナビ運営のSEプラスによる試験対策eラーニングです。

基本情報 プログラミング 言語の選択と学習方法|午後問題の歩き方
update
基本情報のサンプル問題で Python の基礎知識をチェック | 午後問題の歩き方
update
「基本情報 の Python ってどんな感じ?」を解説|午後問題の歩き方
update
矢沢久雄さんが執筆! 午後 プログラミング 問題対策の参考書「速習言語」を刊行しました!!
update
こうすりゃ解ける! 2019年度秋期 (令和元年度) 基本情報技術者試験の午後問題を徹底解説
update
こうすりゃ解ける! 2019年度春期 (平成31年度) 基本情報技術者試験の午後問題を徹底解説
update
こうすりゃ解ける! 2018年度秋期 (平成30年) 基本情報技術者試験の午後問題を徹底解説
update
午後問題の歩き方 | 試験1週間前にやるべき午後問題の知識チェック (チェックシート付き)
update
午後問題の歩き方 | Java プログラミング問題の楽勝パターン(2)オブジェクト指向
update
午後問題の歩き方 | Java プログラミング問題の難易度(1)Java基本構文
update
『プログラムはなぜ動くのか』(日経BP)が大ベストセラー
IT技術を楽しく・分かりやすく教える“自称ソフトウェア芸人”
大手電気メーカーでPCの製造、ソフトハウスでプログラマを経験。独立後、現在はアプリケーションの開発と販売に従事。その傍ら、書籍・雑誌の執筆、またセミナー講師として活躍。軽快な口調で、知識0ベースのITエンジニアや一般書店フェアなどの一般的なPCユーザの講習ではダントツの評価。
お客様の満足を何よりも大切にし、わかりやすい、のせるのが上手い自称ソフトウェア芸人。
主な著作物
- 「プログラムはなぜ動くのか」(日経BP)
- 「コンピュータはなぜ動くのか」(日経BP)
- 「出るとこだけ! 基本情報技術者」 (翔泳社)
- 「ベテランが丁寧に教えてくれる ハードウェアの知識と実務」(翔泳社)
- 「ifとelseの思考術」(ソフトバンククリエイティブ) など多数











