午後問題の歩き方 | 午後問題の読み方~ハードウェア

error
この記事は基本情報技術者試験の旧制度( 2022 年以前)の記事です。
この記事の題材となっている「午後問題」は現在の試験制度では出題されません。 ご注意くださいませ。
筆者は、基本情報技術者試験の対策講座で講師をしています。
もしも、受講者から「ハードウェアの午後問題で1問だけ勉強するとしたら、どれがよいですか?」と質問されたら、平成 25 年度 秋期 午後 問 1「論理演算と加算器」をお勧めするでしょう。
論理演算や加算器に関する問題は、事前に勉強しておけば、短時間に解けるからです。出題頻度も多く、他の問題に応用もできます。
この記事で、問題と解法を示しますので、実際にやってみましょう。
もくじ
論理演算の種類と機能を、あらかじめ知っておこう
以下は、問題の冒頭部分です。
論理演算の種類と機能を一覧表で示していますが、これは、この場で初めて知るような代物ではありません。あらかじめ熟知しておくべきもの です。
それでは、なぜこの一覧表があるのでしょう。
おそらく、設問の前に示すものが、他になかったのでしょう。
論理演算は、真と偽の演算ですが、ここでは、真 を 1 、偽 を 0 で表しています。もしかすると、それだけを示したかったのかもしれません。
- 問 1
- 論理演算と加算器に関する次の記述を読んで,設問 1 ~ 4 に答えよ。
真を 1,偽を 0 として,主要な論理演算の真理値表を,表 1 に示す。 -
表 1 主要な論理演算の真理値表 A B A AND B A OR B A XOR B A NAND B A NOR B 0 0 0 0 0 1 1 0 1 0 1 1 1 0 1 0 0 1 1 1 0 1 1 1 1 0 0 0 A NOT A 0 1 1 0
論理演算が苦手な人のために、論理演算の機能と種類を説明しておきましょう。
論理演算の基本は、AND と OR と NOT です。
これらの機能は、英語の意味そのものであり、AND は「かつ」、OR は「または」、 NOT は「でない」です。
A AND B は、A が 1 かつ B が 1 なら、1 になります。
A OR B は、A が 1 または B が 1 なら、1 になります。
NOT A は、A の値 が 0 なら 1、A の値 が 1 なら 0 になります。
XOR と NAND と NOR は、AND と OR と NOT を組み合わせて実現できる演算なのですが、よく使われるものので、名前が付けられています。
それぞれの名前の意味がわかれば、機能もわかります。
XOR(エックスオア)
eXclusive OR の略で「排他的または」という意味です。
A XOR B は、A が 1 または B が 1 なら、1 になりますが、A と B の 両方 が 1 のときは、0 になります。
つまり、A と B の どちらか一方だけが 1 のとき に、演算結果が 1 になるのです。他方を排除しているので、排他的というわけです。
NAND(ナンド)
NOT AND の略です。
A NAND B は、A AND B の演算結果を NOT 演算します。
つまり、A NAND B = NOT( A AND B )です。
NOR(ノア)
NOT OR の略です。
A NOR B は、A OR B の演算結果を NOT 演算します。
つまり、A NOR B = NOT( A OR B )です。
入力を想定して出力を求める解法では、かなりの時間がかかる
それでは、設問 1 を見てみましょう。NAND と NOR の機能を実現しているのはどれか、という問題です。
- 設問 1
- AND, OR, XOR, NOT の各論理演算を行う論理回路を用いて, NAND と NOR の論理演算を行う論理回路を作成した。次の記述中のに入れる正しい答えを,解答群の中から選べ。ここで, X, Y は 1 ビットの入力, Z は 1 ビットの出力とする。
- NAND の論理回路はaである。
- NOR の論理回路はbである。
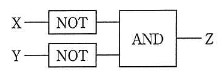
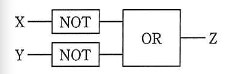
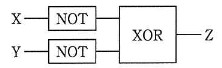
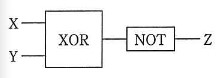
この手の問題の解法は、大きく分けて 2 つあります。
1 つ目の解法は、入力の X と Y に 0 と 1 を想定して、出力の Z を書き出すことです。以下のようになります。
| X | Y | 選択肢アの Z | 選択肢イの Z | 選択肢ウの Z | 選択肢エの Z |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
この結果から、 NAND の機能を実現しているのは、選択肢イであり、 NOR の機能を実現しているのは、選択肢アだとわかります。
しかし、この解法では、かなりの時間がかかってしまいます。
ド・モルガンの法則を知っていれば、短時間で解ける
2 つ目の解法は、以下に示した「ド・モルガンの法則」を使って、式を変形することです。
この解法なら、ほとんど時間がかかりません。
ド・モルガンの法則
【法則 1 】 NOT( X AND Y )= NOT X OR NOT Y
【法則 2 】 NOT( X OR Y )= NOT X AND NOT Y
実は、この設問は、ド・モルガンの法則を知っていれば、式を変形するまでもなく、瞬時に解けてしまいます。
設問が、ド・モルガンの法則そのものになっているからです。
法則1の左辺の NOT( X AND Y )は、X AND Y の NOT なのですから、X NAND Y です。
これが、右辺の NOT X OR NOT Y と等しいのです。
NOT X OR NOT Y は、X と Y それぞれを NOT してから OR しているので、これは選択肢イです。
したがって、選択肢イが NAND です。
法則 2 の左辺の NOT( X OR Y )は、X OR Y の NOT なのですから、X NOR Y です。
これが、右辺の NOT X AND NOT Y と等しいのです。
NOT X AND NOT Y は、X と Y それぞれを NOT してから AND しているので、これは選択肢アです。
したがって、選択肢アが NOR です。
ピンと来ないかもしれないので、ド・モルガンの法則の式に、図を対応付けて示しておきましょう。法則 1 は NAND で、法則 2 は NOR です。
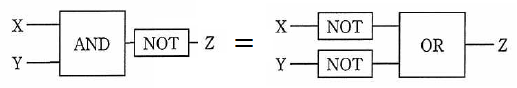
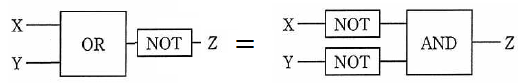
半加算器と全加算器の仕組みも、あらかじめ知っておくべきもの
設問 2 は半加算器に関するもので、設問 3 は全加算器に関するものです。
これらも、この場で初めて知るような代物ではありません。あらかじめ熟知しておくべきものです。
コンピュータの内部では、論理演算を組み合わせて2進数の加算を実現しています。それを実現する装置を、加算器と呼びます。
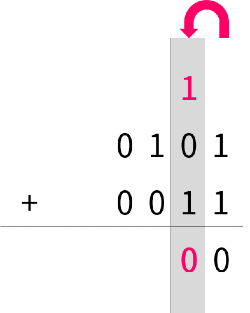
たとえば、 0101 + 0011 という 2 進数の加算を行うとしましょう。
10 進数の加算と同様に、最下位桁から上位桁に向かって、1 桁ずつ順番に足して行きます。最下位桁だけは、その桁にある 2 つの数値を加算します。これを行うのが、半加算器です。
最下位桁より上の桁は、その桁にある2つの数値と、下位桁からの桁上がりの 1 つの数値を加算するので、全部で 3 つの数値を加算します。これを行うのが、全加算器です。
設問 2 では、X と Y を加算し、その結果を C と Z で示しています。
C は桁上がりで、Z は同じ桁の数値です。たとえば、1 + 1 の結果は 10 ですが、10 の 1 が C で、0 が Z です。
- 設問 2
- 各 1 ビットの入力 X, Y を加算して,その結果を各 1 ビットの Z と桁上がり C に出力する “半加算器” の真理値表を表 2 に,論理回路を図 1 に示す。図 1 中のに入れる正しい答えを,解答群の中から選べ。
-
X + Y ------- C Z -
表 2 半加算器の真理値表 X Y C Z 0 0 0 0 0 1 0 1 1 0 0 1 1 1 1 0 -
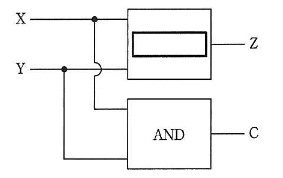
図 1 半加算器の論理回路
解答群
ア AND イ NAND ウ NOR エ OR オ XOR
空欄は、X と Y から Z を得る論理演算を選ぶ問題です。
表 2 を見ると、Z は、X と Y の どちらか一方だけが 1 のときに演算結果が 1 になっているので、これは XOR 演算です。したがって、答えは、選択肢オです。
ただし、半加算器の桁上がりが AND 演算で得られ、同じ桁の数値が XOR 演算で得られることは、あらかじめ熟知しておくべき です。そうすれば、表 2 を見るまでもなく、瞬時に答えがわかります。
全加算器は、2 つの半加算器 と OR 回路で構成される
設問 3 も、全加算器の仕組みを知っていれば、瞬時に答えがわかります。
- 設問 3
- 各 1 ビットの入力 X, Y と,下位桁からの 1 ピットの桁上がり Cin を加算して,その結果を各 1 ビットの Z と桁上がりの C に出力する “全加算器” の真理値表を表 3 に,論理回路を図 2 に示す。図 2 中のに入れる正しい答えを,解答群の中から選べ。
-
X Y + Cin ------- C Z -
β
表 3 全加算器の真理値表 Cin X Y C Z 0 0 0 0 0 0 0 1 0 1 0 1 0 0 1 0 1 1 1 0 1 0 0 0 1 1 0 1 1 0 1 1 0 1 0 1 1 1 1 1 -
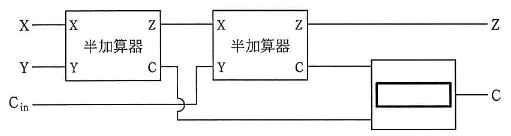
図 2 全加算器の論理回路
解答群
ア AND イ NAND ウ NOR エ OR
全加算器は、3 つの数値を加算します。
全加算器は、2 つの半加算器 と OR 回路で構成されます。
1 つ目の半加算器で 2 つの数値を加算し、その結果の Z と もう 1 つの数値を 2 つ目の半加算器で加算して、最終的な Z を得ます。
2 つの半加算器の桁上がり C の いずれかが 1 なら、最終的な C が 1 になるので、それを OR 回路で検出します。
この仕組みを、あらかじめ熟知しておくべきなのです。設問 3 の答えは、選択肢エ の OR です。
いかがだったでしょう。
ド・モルガンの法則や、半加算器と全加算器の仕組みを知っていれば、設問 1 ~設問 3 を瞬時に解けることがわかったでしょう。
実際の試験問題には、設問 4 もありますが、記事が長くなってしまうので省略します。設問 4 も、論理演算の種類と機能がわかっていれば、ちゃんと解けますので、どうぞご心配なく。
ハードウェアの問題は、早い話が 2 進数と論理演算の問題です。
これは、コンピュータの内部では、10 進数による四則演算ではなく、2 進数を使った論理演算が行われているからです。
2 進数と論理演算を苦手にしている人が多いようですが、コンピュータの根本的な動作原理なので、ぜひマスターしてください。
ちゃんとマスターすれば、どの問題でも短時間に解けますよ。
それではまた、お会いしましょう!
label 関連タグ
免除試験を受けた 74.9% の方が、科目A免除資格を得ています。
※独習ゼミは、受験ナビ運営のSEプラスによる試験対策eラーニングです。

基本情報 プログラミング 言語の選択と学習方法|午後問題の歩き方
update
基本情報のサンプル問題で Python の基礎知識をチェック | 午後問題の歩き方
update
「基本情報 の Python ってどんな感じ?」を解説|午後問題の歩き方
update
矢沢久雄さんが執筆! 午後 プログラミング 問題対策の参考書「速習言語」を刊行しました!!
update
こうすりゃ解ける! 2019年度秋期 (令和元年度) 基本情報技術者試験の午後問題を徹底解説
update
こうすりゃ解ける! 2019年度春期 (平成31年度) 基本情報技術者試験の午後問題を徹底解説
update
こうすりゃ解ける! 2018年度秋期 (平成30年) 基本情報技術者試験の午後問題を徹底解説
update
午後問題の歩き方 | 試験1週間前にやるべき午後問題の知識チェック (チェックシート付き)
update
午後問題の歩き方 | Java プログラミング問題の楽勝パターン(2)オブジェクト指向
update
午後問題の歩き方 | Java プログラミング問題の難易度(1)Java基本構文
update
『プログラムはなぜ動くのか』(日経BP)が大ベストセラー
IT技術を楽しく・分かりやすく教える“自称ソフトウェア芸人”
大手電気メーカーでPCの製造、ソフトハウスでプログラマを経験。独立後、現在はアプリケーションの開発と販売に従事。その傍ら、書籍・雑誌の執筆、またセミナー講師として活躍。軽快な口調で、知識0ベースのITエンジニアや一般書店フェアなどの一般的なPCユーザの講習ではダントツの評価。
お客様の満足を何よりも大切にし、わかりやすい、のせるのが上手い自称ソフトウェア芸人。
主な著作物
- 「プログラムはなぜ動くのか」(日経BP)
- 「コンピュータはなぜ動くのか」(日経BP)
- 「出るとこだけ! 基本情報技術者」 (翔泳社)
- 「ベテランが丁寧に教えてくれる ハードウェアの知識と実務」(翔泳社)
- 「ifとelseの思考術」(ソフトバンククリエイティブ) など多数










