午後問題の歩き方 ｜ 矢沢久雄の アルゴリズム問題の解き方（2）

矢沢 久雄
2022-11-28 更新

前回の記事では、午後試験のアルゴリズム問題を克服する最終ステップとして、ひたすら過去問題を練習して自分流の解法を見出す、というアドバイスしました。

今回の記事では、自分流の解法の例を紹介します。

これは、私流の解法ですので、皆さん流の解法を見出すための参考にしてください。

すぐに設問と選択肢を見て、答えを得るために必要なことを知る

ここでは、アルゴリズム問題の例として、平成 22 年度 春期 午後 問 8「マージソート」を取り上げます。

マージソートは、試験のシラバスに示されている基本アルゴリズムの 1 つです。

配列を要素数が 1 個になるまで分割し、それらを結合（ merge ＝ 結合）することを繰り返して、全体をソートします。あらかじめ、この手順を知っている必要があります。

試験問題を全て掲載しますが、ポイントとなる部分だけを見てください（もしも、きちんと解くと 30 分ぐらいかかっちゃいますよ）。

アルゴリズム問題は、

の順に構成されています。プログラムを隅々まで理解するのではなく、設問に答えることが目的なので、プログラムの説明とプログラムにざっと目を通したら、すぐに設問を見ることが重要 です。

以下が、この問題の設問です。

問題とプログラムは、あとで示します。基本情報技術者試験の問題は、すべて選択問題です。したがって、選択肢が大きなヒントになります。とにかく選択肢をよく見てください。

ア　(i < num1) and (j < num2)
イ　(i < num1) or (j < num2)
ウ　(j < num1) and (i < num2)
エ　(j < num1) or (i < num2)
オ　(i + j) < (num1 + num2)
カ　(i + j) ≦ (num1 + num2)
キ　(i + j) > (num1 + num2)
ク　(i + j) ≧ (num1 + num2)

ア　2 → 3 → 2,3 → 2,3,8 → 1 → 5 → 1,5 → 1,5,7 → 1,2,3,5,7,8
イ　3 → 8 → 3,8 → 2,3,8 → 7 → 5 → 7,5 → 1,5,7 → 1,2,3,5,7,8
ウ　2,8 → 2,3,8 → 1,5 → 1,5,7 → 1,2,3,5,7,8
エ　3,8 → 2,3,8 → 7,5 → 1,5,7 → 1,2,3,5,7,8
オ　2,3,8 → 1,5,7 → 1,2,3,5,7,8
カ　3,8,2 → 7,5,1 → 1,2,3,5,7,8

■ i < num1
| ･list[i] + slisti[i]
| ･i ← i + 1
■
■ j < num2
| ･list[j] ← slist2[j]
| ･j ← j + 1
■

■ i < num1
| ･list[i + num1] ← slist1[i]
| ･i ← i + 1
■
■ j < num2
| ･list[j + num2] ← slist2[j]
| ･j ← j + 1
■

■ i < num1
| ･list[j + num1] ← slisti[i]
| ･i ← i + 1
■
■ j < num2
| ･list[i + num2] ← slist2[j]
| ･j ← j + 1
■

■ i < num1
| ･list[i + num2] ← slist1[i]
| ･i ← i + 1
■
■ j< num2
| ･list[j + num1] ← slist2[j]
| ･j ← j + 1
■

ア
■ i < num1
| ･list[i] + slisti[i]
| ･i ← i + 1
■
■ j < num2
| ･list[j] ← slist2[j]
| ･j ← j + 1
■

イ
■ i < num1
| ･list[i + num1] ← slist1[i]
| ･i ← i + 1
■
■ j < num2
| ･list[j + num2] ← slist2[j]
| ･j ← j + 1
■

ウ
■ i < num1
| ･list[j + num1] ← slisti[i]
| ･i ← i + 1
■
■ j < num2
| ･list[i + num2] ← slist2[j]
| ･j ← j + 1
■

エ
■ i < num1
| ･list[i + num2] ← slist1[i]
| ･i ← i + 1
■
■ j < num2
| ･list[j + num1] ← slist2[j]
| ･j ← j + 1
■

このように、設問と選択肢を見ることで、答えを得るために何が必要なのかがわかります。その必要なことを見つけるために、プログラムの説明とプログラムを見るのです。

これが、アルゴリズム問題の基本的な解法です。

具体例を想定してプログラムの説明を読む

以下に、プログラムの説明を示します。プログラムの説明を読むときに大事なのは、具体例を想定すること です。

この問題では、配列 list に格納された num 個のデータを昇順にソートしますが、num 個では、プログラムの説明がよくわからないでしょう。

num 個に具体的な値を想定してみましょう。

もしも、問題に具体例が示されている場合は、素直にそれを想定しましょう。

出題者は、「制限時間内に問題を解くためのヒントをあげよう」と考えて、具体例を示している からです。

この問題では、num ＝ 7 個とした具体例が示されているので、それを想定してください。

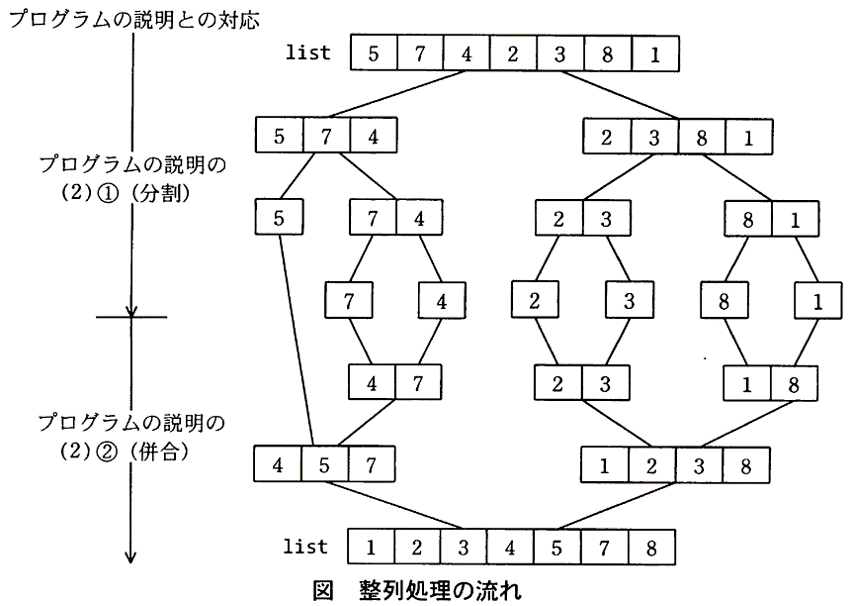
num ＝ 7 個という具体例を想定すると、プログラムの説明が、とてもわかりやすくなります。

たとえば、プログラムの説明の（2）の ① にある

これは num ＝ 7 個を想定すると、

と読むことができます。とてもわかりやすいでしょう。

searchタグで関連記事をチェック　テクニック 具体的な値を想定

プログラムは、具体例を想定したプログラムの説明と対応付けて読む

プログラムを読むときは、具体例を想定したプログラムの説明と対応付けて読んでください。そうすると、「この穴埋めでは、こういう処理を行えばよいのだ！」と気付きます。

以下に、プログラムを示します。

このプログラムは、Sort 関数 と Merge 関数 から構成されています（試験問題では、関数を副プログラムや手続と呼ぶ場合もあります）。

先ほど示したプログラムの説明の（2）は、Sort 関数 の説明であり、（3）は Merge 関数 の説明です。

〔プログラム〕

announcement横にスクロールできます

/* プログラム Sort */
○Sort(整数型: list[], 整数型: num)
○整数型: i, num1, num2
○整数型: slist1[], slist2[]               /* 配列の宣言 */
▲ a
|　・num1 ← num ÷ 2                       /* slist1 の要素数計算 */
|　・num2 ← num - num1                    /* slist2 の要素数計算 */
|　■　i:0, i < num1, 1 
|　|　・slist1[i] + list[i]
|　■
|
|　■　i:0, i < num2, 1
|　|　・slist2[i] ← b
|　■
|　・Sort(slisti, num1)
|　・Sort(slist2, num2)
|　・Merge(slisti, num1, slist2, num2, list)
▼　        arrow_back－－－－－－－－－－－－－－－－－ α
/* プログラム Sort の終わり */

/* 副プログラム Merge */
○Merge(整数型: slisti[], 整数型: num1,
　　　　整数型: slist2[], 整数型: num2,
　　　　整数型: list[] )
○整数型: i, j
・i ← 0
・j ← 0
■ c
|　▲ slist1[i] < slist2[j]
|　|　・list[i + j] ← slisti[i]
|　|　・i ← i + 1
|　+
|　|　・list[i + j] ← slist2[j]
|　|　・j ← j + 1
|　▼
■
■ (i < num1) or (j < num2)
|　▲ i < num1
|　|　・list[i + j] ← slist1[i]
|　|　・i ← i + 1
|　+arrow_back－－－－－－－ β
|　|　・list[i + j] ← slist2[j]
|　|　・j ← j + 1
|　▼
■
  /* 副プログラム Merge の終わり */

プログラムの説明の（2）に「この再帰的な呼び出しは、引数で渡される配列 list のデータの個数が 1 になると終了する」とあります。

「再帰的な呼び出し」とは、関数の処理の中で同じ関数を呼び出すことによって、繰り返しを実現するテクニックです。

この説明と対応付けて Sort 関数 のプログラムを見ると、確かに Sort 関数 の処理の中で Sort 関数 を呼び出している部分があります。

それによって「空欄 a は、再帰呼び出しを続ける条件だ！」と気付きます。

気付いたら、設問の選択肢を見てみましょう。

「この再帰的な呼び出しは、引数で渡される 配列 list の データの個数 が 1 になると 終了する」の
「引数で渡される 配列 list の データの個数」とは、num のことです。

「num が 1 になると 終了する」のですから、
「num が 1 より大きければ 再帰呼び出しを続ける 」です。

これに該当する選択肢は、ウです。

繰り返し処理の穴埋めは、繰り返しの最初の処理を想定すればわかる

「繰り返し処理を読み取るのが苦手」という人が多いでしょう。

よい解法があります。

繰り返しの最初の処理を想定するのです。

そうすれば、繰り返し処理の中にある穴埋めに、何が入るか簡単にわかります。

繰り返しの穴埋めは、繰り返しのどの時点でも成り立つのですから、最もわかりやすい最初の処理を想定するのです。

この問題では、

という手順を繰り返していますが、最初の要素数 7 個の配列を 3 個と 4 個に分割する処理を想定して、プログラムを読んでみましょう。

そうすれば、プログラムの空欄 b の穴埋めができます。

|　■　i:0, i < num1, 1 
|　|　・slist1[i] + list[i]
|　■
|
|　■　i:0, i < num2, 1
|　|　・slist2[i] ← b
|　■

このコピーにおいても、繰り返しの最初の処理を想定して、slist[0] に list[3] をコピーしているものを選択肢の中から選びます。

繰り返しの最初なのですから i = 0 です。

i = 0 で list の [ ] の中が 3 になるのは、選択肢ウ の list[num1 + i] です。num1 ＝ 3 だからです。

いかがでしょう。

繰り返しの最初の処理を想定すると、簡単に答えを選べることがわかったでしょう。

過去問題を練習しながら、このように自分流の解法を見出す経験を積み重ねて行けば、アルゴリズム問題を克服できるはずです。

説明が長くなってしまうので、他の設問の解法の説明は省略しますが、ぜひ自分流でやってみてください。

以下に、解答とアルゴリズム問題の出題傾向に関する記事を示しておきます。

設問 1　a －ウ、b －ウ、c －ア
設問 2　ウ
設問 3　エ

label アルゴリズム問題の出題傾向

アルゴリズム及びデータ構造の出題傾向（午後問8）

午後試験のアルゴリズム問題の制限時間の目安は、令和元年以前の過去問であれば、 150 分 ×（ 20 点 ／ 100 点）＝ 30 分 です ^注。

他人が作ったプログラムを 30 分で理解するのは、はっきり言って困難 でしょう。

プログラムを隅々まで完璧に理解しようなどと思わずに、「問題が解ければいいのだ」と割り切ることが大事です。

設問が解ければよいのです。選択肢から答えを選べればよいのです。

そう思うと、前回の記事で紹介した某講師の「選択肢だけを見て答えを選ぶ」という解法にも、一理あるような気がします。ただし、「選択肢を見て大いにヒントにする」ならです。

それでは、またお会いしましょう！

^注令和 2 年以降は配点が変更され 150 分 × ( 25 点 / 100 点) = 37.5 分 になります

info編集部よりお知らせ
アルゴリズム問題のトレースのコツなど紹介する連載が始まりました！

アルゴリズム問題を解くコツ

基本情報 プログラミング 言語の選択と学習方法｜午後問題の歩き方

update 2022-11-28

基本情報のサンプル問題で Python の基礎知識をチェック | 午後問題の歩き方

update 2020-09-04

「基本情報 の Python ってどんな感じ？」を解説｜午後問題の歩き方

update 2020-10-14

矢沢久雄さんが執筆! 午後 プログラミング 問題対策の参考書「速習言語」を刊行しました!!

update 2023-05-22

こうすりゃ解ける！ 2019年度秋期 (令和元年度) 基本情報技術者試験の午後問題を徹底解説

update 2022-02-15

こうすりゃ解ける！ 2019年度春期 (平成31年度) 基本情報技術者試験の午後問題を徹底解説

update 2021-01-08

こうすりゃ解ける！ 2018年度秋期 (平成30年) 基本情報技術者試験の午後問題を徹底解説

update 2021-09-15

午後問題の歩き方 ｜ 試験1週間前にやるべき午後問題の知識チェック (チェックシート付き)

update 2021-09-15

午後問題の歩き方 ｜ Java プログラミング問題の楽勝パターン（2）オブジェクト指向

update 2022-06-07

午後問題の歩き方 ｜ Java プログラミング問題の難易度（1）Java基本構文

update 2022-06-07

矢沢 久雄

『プログラムはなぜ動くのか』（日経BP）が大ベストセラー
IT技術を楽しく・分かりやすく教える“自称ソフトウェア芸人”

大手電気メーカーでＰＣの製造、ソフトハウスでプログラマを経験。独立後、現在はアプリケーションの開発と販売に従事。その傍ら、書籍・雑誌の執筆、またセミナー講師として活躍。軽快な口調で、知識０ベースのＩＴエンジニアや一般書店フェアなどの一般的なＰＣユーザの講習ではダントツの評価。
お客様の満足を何よりも大切にし、わかりやすい、のせるのが上手い自称ソフトウェア芸人。

主な著作物

• 「プログラムはなぜ動くのか」（日経BP）
• 「コンピュータはなぜ動くのか」（日経BP）
• 「出るとこだけ! 基本情報技術者」 (翔泳社)
• 「ベテランが丁寧に教えてくれる ハードウェアの知識と実務」（翔泳社）
• 「ｉｆとｅｌｓｅの思考術」（ソフトバンククリエイティブ）　など多数