2の補数表現｜やさしい基礎理論

矢沢久雄
2024-03-26 更新

この連載は、基本情報技術者試験の受験者を対象としたものです。

多くの受験者が苦手としている「情報の基礎理論」の分野から毎回1つずつテーマをあげて、やさしくポイント解説と問題解説を行います。苦手分野を克服して、試験の得点をアップしましょう。

今回のテーマは、 2の補数表現です。

1 2の補数表現とは？
2 反転して1を足す
3 符号ありと符号なし
4 2の補数表現に関する問題の例（その1）
5 2の補数表現に関する問題の例（その2）

2の補数表現とは？

コンピュータの内部では、電圧の高低を1と0に対応付けた2進数で、あらゆる情報を表しています。１と0だけですから、そのままではマイナスの数を表すことができません。

たとえば、8ビット（8桁）の2進数で表せるのは、00000000～11111111という0以上のプラスの数です。しかし、マイナスの数が取り扱えないのでは不便です。そこで、1と0だけでマイナスの数を表す方法が、いくつか考案されています。2の補数表現は、整数のマイナスの数を表す代表的な方法です。
2の補数表現を理解するポイントは、コンピュータの内部では、取り扱える情報の桁数が固定されていて（この桁数は、データを伝える電線の数や、ディジタルICの内部にあるデータの格納領域の桁数です）、その桁数を超えた情報は消える、ということです。
たとえば、8ビットでデータを取り扱うなら、9ビット目に桁上がりしたデータは消えます。

2の補数表現の仕組みを説明する定番の例として「8ビットのデータの11111111は、マイナス1である」があります。なぜ11111111がマイナス1なのでしょう。

図1に示したように、11111111に00000001を足してみましょう。

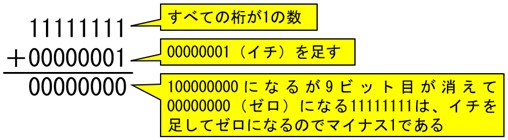
結果は、9ビット目に桁上がりして100000000になりますが、データが8ビットなのですから、9ビット目の1が消えて00000000になります。11111111は、00000001（イチ）を足して00000000（ゼロ）になるのですから、マイナス1なのです。
「ある数に足してゼロになる数は、もとの数のマイナスの数であるとみなせる」というのが、2の補数表現の仕組みです。

こんな方法で正しい演算結果が得られるのか？と思われるかもしれませんが、ちゃんと正しい演算結果が得られます。

反転して1を足す

10進数のマイナスの数を、2の補数表現の2進数に変換する方法を説明しましょう。

例として、10進数のマイナス2を、8ビットの2進数に変換してみます。
10進数のプラス2を8ビットの2進数に変換すると（10進数と2進数の変換方法は、この連載の第1回で説明しています）、00000010です。この数に足してゼロになる数がマイナス00000010です。その数を得るには「反転して1を足す」という操作を行います。

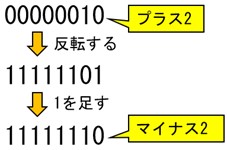
00000010を反転する（0を1に、1を0にする）と、11111101になります。
00000010と11111101を足すと、すべての桁が1の11111111になります。
それでは、00000010を反転して、さらに1を足した11111110を足すとどうなるでしょう。すべての桁が1の11111111より1つ大きな数になり、9ビット目に桁上がりして100000000ですが、データが8ビットなので9ビット目が消えて00000000（ゼロ）になります。
つまり、反転して1を足すと、もとの数に足してゼロになる数が得られるのです。これは、もとの数のマイナスの数です。反転して1を足して、もとの数のマイナスの数を得る手順を図2に示します。

符号ありと符号なし

2の補数表現を使うかどうかは、プログラムを作るときに設定できます（設定方法は、プログラミング言語や環境によって異なります）。
たとえば、8ビットの11111111は、2の補数表現を使わなければ10進数で255であり、2の補数表現を使えば１０進数でマイナス1です。 2の補数表現を使うことを「符号あり」と呼び、 2の補数表現を使わないことを「符号なし」と呼びます。

符号なしの場合は、8ビットの2進数で表せる00000000～11111111は、10進数の0～255であり、すべて0以上のプラスの数です。
符号ありの場合は、プラスとマイナスの両方の数を取り扱えるように、最上位桁が0の00000000～01111111を0以上のプラスの数とし、最上位桁が1の11111111～10000000を2の補数表現のマイナスの数とする約束になっています。符号ありでは、最上位桁が0ならプラスであり、最上桁が1ならマイナスです。最上位桁を見ればプラスかマイナスかがわかるので、最上位桁のことを「符号ビット」と呼びます。

符号ビットが0の0000000～01111111は、10進数で0～127です。それでは、符号ビットが1の11111111～10000000は、10進数に変換するとどうなるでしょう。

11111111は、これまでに説明したようにマイナス１です。10000000がいつくかは、「マイナスのマイナスはプラスである」という考え方で、プラスの数にしてみればわかります。プラスの数を反転して1を足すとマイナスの数になります（足すとゼロになる数が得られるからです）。それなら、マイナスの数を反転して1を足すとプラスの数になります（足すとゼロになる数が得られるからです）。10000000を反転すると01111111になり、さらに1を足すと10000000になります。これをプラスの数として10進数に変換すると128です。したがって、10000000は128に足してゼロになる数であり、マイナス128です。したがって、11111111～10000000は、10進数でマイナス1～マイナス128です。

2の補数表現に関する問題の例（その1）

2の補数表現に関する問題を2つほど紹介しましょう。
はじめは、10進数のマイナスの小数点数を、2の補数表現の2進数に変換する問題です。

問題例１（出典：H23秋問2）

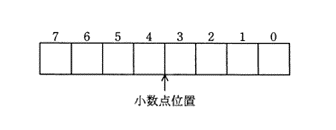
10進数-5.625を，8ビット固定小数点形式による2進数で表したものはどれか。ここで，小数点位置は3ビット目と4ビット目の間とし，負数には2の補数表現を用いる。

ア：01001100　　イ：10100101　　ウ：10100110　　エ：11010011

＜解説＞

固定小数点形式とは、特定の桁位置に小数点があるとして、整数で小数点数を表す形式です。ここでは、8ビットの2進数の3ビット目と4ビット目の間に小数点があるとするので、たとえば、01100101という整数が0100.0101という小数点数を表します。

－5.625という負の10進数を、一気にマイナスの2進数に変換するのは困難でしょう。5.625というプラスの10進数を2進数に変換して、それを2の補数表現でマイナスの数にすれば簡単です。
この問題の2進数は8ビットであり、整数部が4ビットで、小数点以下が4ビットです。整数部が4ビットの桁の重みは、1ビット目が1で、桁が上がると2倍になるので、8、4、2、1です。5.625の整数部の5は、5＝4＋1なので、2進数で0101です。小数点以下の4ビットの桁の重みは、整数部の1ビット目が１で、桁が下がると1/2になるので、0.5、0.25、0.125、0.0625です。5.625の小数点以下の0.625は、0.625＝0.5＋0.125なので、2進数で0.1010です。
したがって、10進数の0.625は2進数で0101.1010であり、この問題に示された固定小数点形式では、01011010です。01011010を反転して1を足した10100110が、－5.625です。

したがって、選択肢ウが正解です。

2の補数表現に関する問題の例（その2）

次は、10進数のマイナスの数を2の補数表現に変換し、さらに、それを符号なしと解釈したら10進数でいくつになるか、という問題です。

問題例２（出典：H17春問3）

負数を2の補数で表す8ビットの数値がある。この値を10進数で表現すると－100である。この値を符号なしの数値として解釈すると，10進数で幾らか。

ア：２８　　イ：１００　　ウ：１５６　　エ：２２８

＜解説＞

8ビットの2進数の桁の重みは、128、64、32、16、8、4、2、1です。
100＝64＋32＋4なので、2進数で01100100です。01100100を反転して1を足した10011100が、－100です。この10011100を符号なしとみなすと、128、16、8、4の桁が1なので、10進数で128＋16＋8＋4＝156です。

したがって、選択肢ウが正解です。

＊　　　　＊　　　　＊

基本情報技術者試験の公開問題を見ると、過去に出題された問題の再利用が多いことがわかります。
したがって、試験に合格するために最も効率的で効果的な学習方法は、できなかった問題があれば、できるようになるまで練習することです。もしも、今回取り上げた問題がすぐにできなかったら、できるようになるまで練習してください。

それでは、またお会いしましょう！