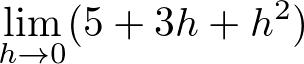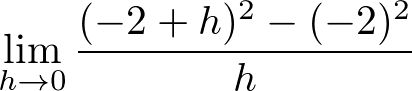AI･機械学習に入門するためのやり直し数学「微分・積分の基礎」 研修コースに参加してみた

Learning Topics 編集部

今回参加した研修コースは AI･機械学習に入門するためのやり直し数学「微分・積分の基礎」 です。

いつかレポートすることになるのではないかと、戦々恐々としていましたが、やってきました。。

n 年ぶりの微分・積分です。( n は 2 ケタとだけ申し上げておきます)

機械学習の記事で数式が出るたびに、そっ閉じしていた私ですが、参加してみると、なぜ微分・積分を使うのかわかり、丁寧にステップを踏んで解説頂いたので、 n 年ぶりに “わかる、わかるぞー” という感覚になりました!

機械学習で数式を見るたびに、「いつかやる」と思っていた方にはとてもオススメです!!

では、どんな内容だったのかレポートします!!

コース情報

講師紹介

Python で機械学習入門 につづき、 米山 学 さん が登壇されました。

米山 学
JavaはもちろんPython/PHPなどスクリプト言語､Vue/ReactなどJSだってなんだってテックが大好き。原点をおさえた実践演習で人気

微分・積分のような数学を研修で学ぶのは何か不思議な気がします。

今日の内容

• 微積は数II
  • 会場でも2人だけがやってらっしゃいました
  • やったとしても忘れてる方が多い
• それほど難しいものは用意してません

AI / 機械学習 / データサイエンスと微積

まずは簡単に微積の関係を触れました。

• AI･機械学習･データサイエンスに必要な数学
  • 微積
  • 線形代数
    • 行列・ベクトル
  • 確率/統計
    • データサイエンスは統計
    • 45 歳以上の方は、実は、統計を数学でやっていない (!!)

このうち、今日は微積をやります。ドキドキ。。

統計について

• 統計は2つある
  • 記述統計学
    • データの特徴を出す
  • 数理統計学
    • データの分析や予測/推測
    • データサイエンスで使うのはこっち
    • 推測統計学 と 多変量解析 にわかれる
      • Deep Learning は多変量解析
• 機械学習
  • 予測モデルを作る
    • x -> y
    • 1 -> 2 / 2 -> 4 / 3 -> 6 から -> が何かを探る
  • x -> y のような入出力のデータセットを教師データと言う
• 予測モデルの表現
  • 関数として表現される
  • グラフ (直線/曲線) で表現できる
  • 値の予測に使うのが微分
  • 予測値が発生する確率に使うのが積分
  • 機械学習のアルゴリズムでは単純な微積は使ってないが、その応用
• 微分とは
  • 曲線の傾きを求める
• 積分
  • 特に曲線の面積を求めるのが積分の役割

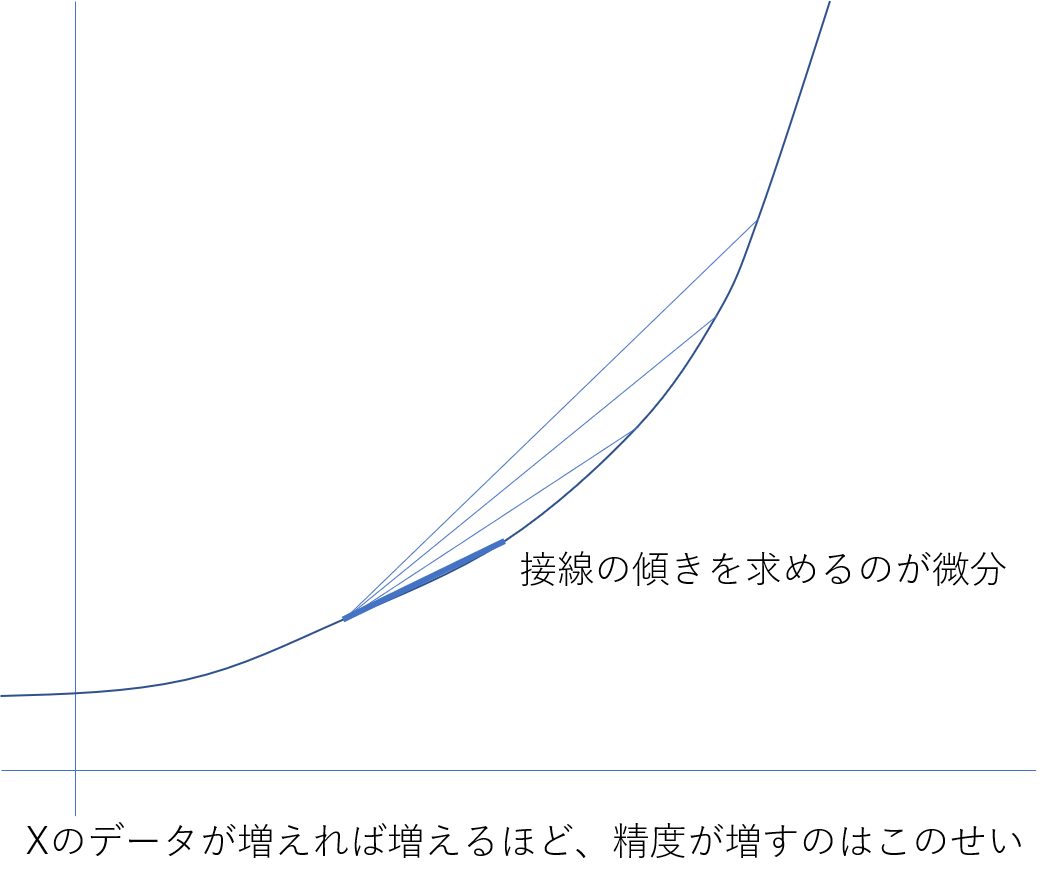
なるほど、予測モデルとは関数で表現するのですね。(まったくの素人…)

微分とは

• f(x) -> (微分) -> f'(x) を求めるというのが数学上の定義
• この f'(x) を導関数という
  • 微分係数を一般化するための関数
  • 微分係数とは平均変化率の極限値

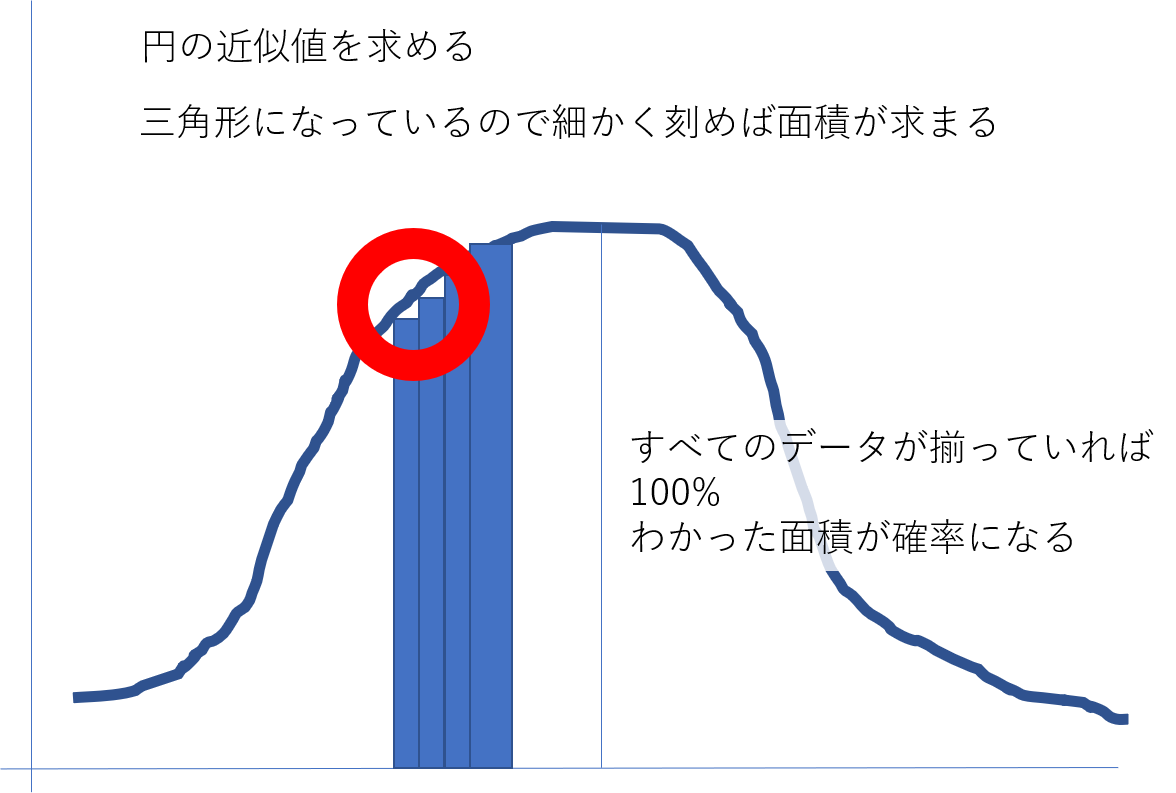
米山さんにホワイトボードを使って図示されて、わかるようになってきました。

平均変化率の計算

直線のグラフで x が 1 増加すると、 y がどれぐらい増加するのか、それを表したのが平均変化率です。

• 平均変化率の公式　

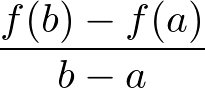
例題

以下の関数において、x の値が 2 から 4 まで変化する場合の平均変化率を求めよ。またそれぞれのグラフを記述せよ。

1. y = x
2. y = 2x
3. y = x²

平均変化率の極限値

では、曲線における、ある1点の平均変化率を求めるにはどうするとよいのでしょう。

そこで出てくるのが極限値です。

• y=f(x) において、 x の値を限りなく a に近づけた場合に f(x) の値が限りなく b に近づくこと
• この b を「極限値」(limit)と呼ぶ
• 極限値を limit と呼ぶ
• 次のように表される　

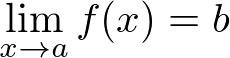
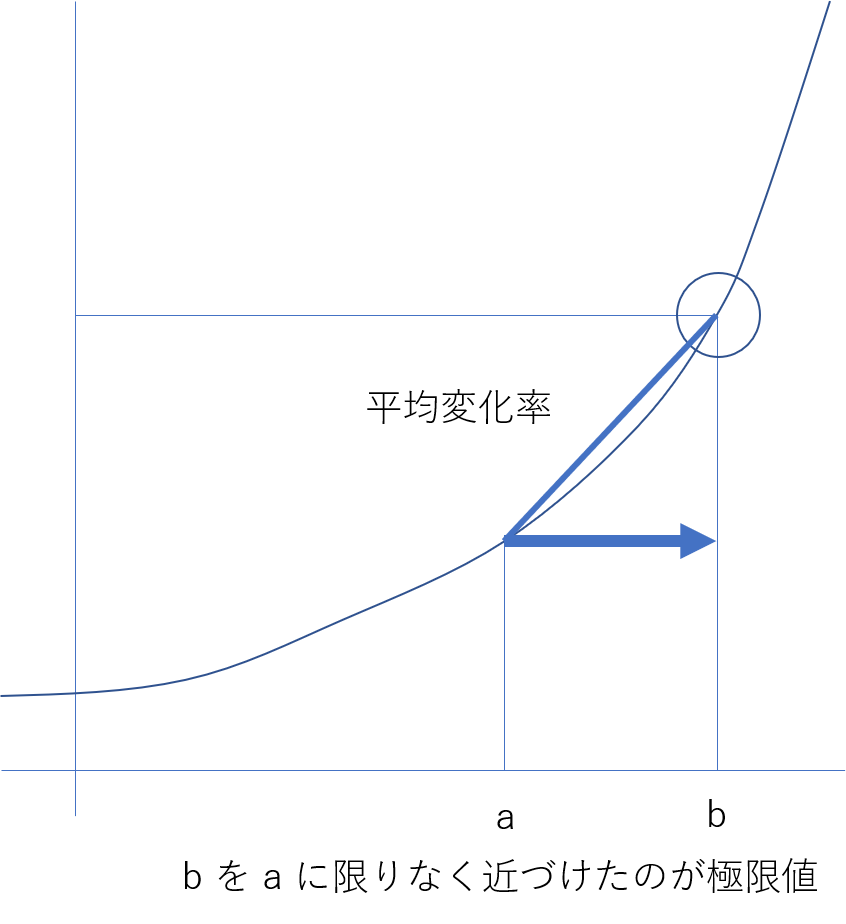
例題

次の極限値を求めよ

微分係数で傾きを求める

微分係数は 特定の値 における傾きを出すものです。

• 微分係数は平均変化率の極限値とも考えられる
• 平均変化率の公式から考える
• グラフにするとわかりやすい

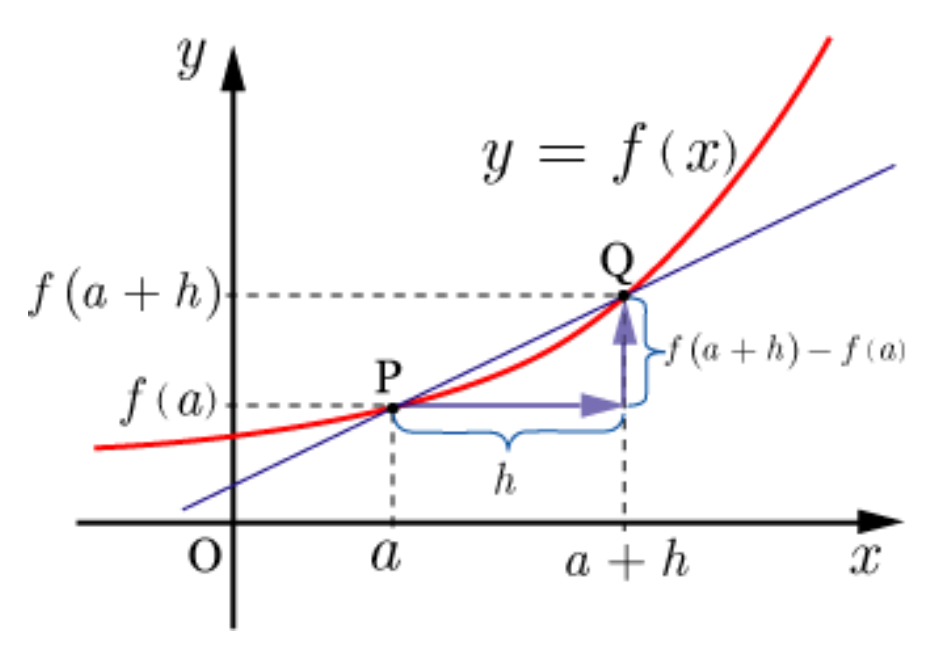
• 微分係数の公式
  
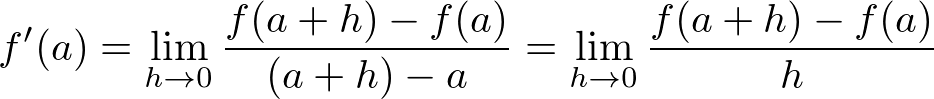
  • 慣習的に 増加した値 を h とする

例題

導関数

微分係数がある特定の値における傾きだったのに対して、どの値でも微分係数が求まる、というのが導関数です。

• 導関数を求めることを「微分する」という
• どんな点を取り出しても傾きがわかる「汎用的な関数」
• 導関数を求める基本公式　

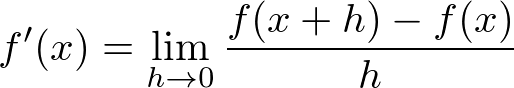
いやぁ、すごいですね、導関数。
高校のときに、もうちょっとやっていればよかったと思います。。(当時はまったくモチベーションがわかなかった…)

ちなみに、導関数の話を聞きながら、ちょっと再帰的だなぁと思いました。
なお、わたしは再帰、苦手です。。

(さらに、ちなみに再帰はプログラマの適性を測るときに使えるそうです…察し)

例題

積分

今度は微分で求めた予測値が、どれぐらいの確率で当たるのか、それを求めるのが積分です。
ちなみに、これを書きながらお天気の降水確率っぽいな、と思いました。 (小並感)

• 微分したものをもとに戻すのが積分
• 不定積分と定積分がある
  • x の値を定数でやるのが 定積分
  • x の値を変数でやるのが 不定積分
• 積分を使うと、a の値が決まったときに b の値が定まる範囲 = 面積 が求められる

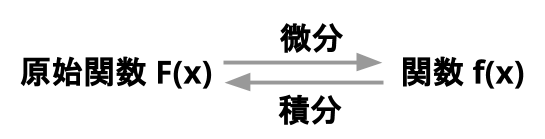
不定積分

• 不定積分の関係式　
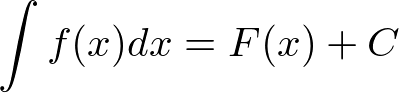
• ある関数 f(x) の不定積分（原始関数）の 1 つを F(x)
• C は定数項で「積分定数」という
• 記号 ∫ はインテグラルと読む
• dx は “xで積分する” という意味

• 不定積分の基本公式
  

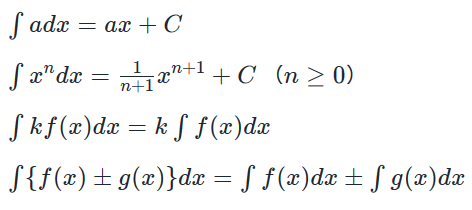
例題

次の不定積分を求めよ。

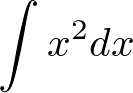
定積分

• 定積分の定義　F'(x) = f(x) のとき　

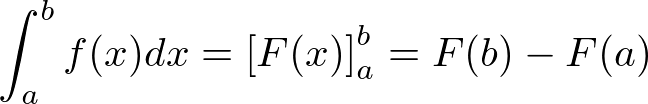
• a -> b の値が変化したときの面積を求める
  • 値が求まる
  • 不定積分は関数が求まる

例題

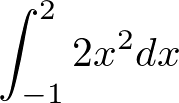
この定積分で -1 から 2 まで値が変化したときの ( x = 0 との) 面積が求まりました

グラフ上の関数と面積

何らかの関数や x 軸との面積の求め方を学習しました。

例題

例題

なお、実際の機械学習はもっとややこしい微分・積分を使っていて、3 次元の微分 (偏微分) が出てくるそうです。（お、おう。)

この面積の求め方を学習したところで、このコースは修了しました。

まとめ

このコースではAI･機械学習･データサイエンスの基礎となる簡単な微分・積分について、どう使っているのか、どう計算するのか、学習しました。

n年ぶりに微分と積分をやったのですが (n年前は挫折して諦めた) 、改めてやってみると、とても面白いものでした。久しぶりに、わかるという、心地よい感覚がありました。

これで自分の子どもたちにも微積をやるモチベーションを伝えられますw (教えられる訳ではない)。

ちなみに、私の理解の整理と確認を助けてくれたチームの大石くんにはとても感謝です。ありがとう!!!

数式出てくるたびに、そっ閉じしている方にはとてもオススメです !!!

label SE カレッジの無料見学、資料請求などお問い合わせはこちらから!!

label SEカレッジを詳しく知りたいという方はこちらから !!

SEカレッジ
IT専門の定額制研修　月額28,000円 ～/ 1社 で IT研修 制度を導入できます。
年間 670 講座をほぼ毎日開催中!!

Learning Topics 編集部

SEプラスにしかないコンテンツや、研修サービスの運営情報を発信しています。