エクセルでわかる統計・データサイエンスで使う数学の基礎|研修コースに参加してみた

今回参加したコースは エクセルでわかる統計・データサイエンスで使う数学の基礎 です。
実はわたくし統計が苦手でして … 。 「場合の数」からして「これ、必要?」と思って苦手になり、数式が出てくるころには理系を断念して、避けて通ってきた人生でした。 将来、これが必須な時代になるよと言ってくれていれば。
そんなわたしがこのコースを受講してみたところ、「えっ、数式わからんでも、 Excel 様がなんとかしてくれるやん」「あ、この手法使えば、あのデータでいい感じにできるかも」と、とても前のめりに統計やデータサイエンスをやる気になりました!
では、どんなコースだったのか、レポートします!
コース情報
| 想定している受講者 | 特になし |
|---|---|
| 受講目標 | 平均や分散といった統計の基本推定や検定、回帰分析といった応用まで、 Excel だけでできる分析方法を身につける |
講師紹介
コースの講師は、アルゴリズム力をやさしく鍛えられるヒット書籍 “プログラマ脳を鍛える数学パズル” の著者、 増井 敏克さんが登壇されました。 この “参加してみた” レポートでは初めての登場です。
増井 敏克
増井技術士事務所 代表 / 技術士(情報工学部門)
1979 年奈良県生まれ。 大阪府立大学大学院修了。 テクニカルエンジニア(ネットワーク、情報セキュリティ)、その他情報処理技術者試験にも多数合格。 また、ビジネス数学検定 1 級に合格し、公益財団法人日本数学検定協会認定トレーナーとしても活動。 「ビジネス」×「数学」×「 IT 」を組み合わせ、コンピュータを「正しく」「効率よく」使うためのスキルアップ支援や、各種ソフトウェアの開発を行っている。
「図解まるわかり データサイエンスのしくみ」(翔泳社 刊)
「図解まるわかり セキュリティのしくみ」(翔泳社 刊)
「 IT 用語図鑑 ビジネスで使える厳選キーワード 256 」(翔泳社 刊)
「図解まるわかり アルゴリズムのしくみ」(翔泳社 刊)
「プログラマ脳を鍛える数学パズル シンプルで高速なコードが書けるようになる 70 問」(翔泳社 刊)
個人的には増井さんといえば、 CodeIQ の出題者というイメージが強いです。 CodeIQ いいサービスでした(若干、年齢バレ)。 プロコンではない、こういうサービス、創ってみたいなぁ。
私の感慨はさておき、早速、今日のコースでやることを紹介いただきました。
- 数学検定協会が定義する 5 つの力に基づいて実施
- 把握力、分析力、選択力、予測力、表現力
データ分析とは
まずはデータ分析を行う理由から順序立てて解説いただきました。
- なぜ、データ分析をするのか?
- データ分析で KKD (経験・勘・度胸)に根拠を示すこと
- データを使うとは?
- 統計学は少ないデータでも高い精度で予測する
- ビッグデータは大量のデータから未知の発見をする
- 統計学とビッグデータの考えは離れているように感じる
- 今日は統計がテーマ
- データ分析の流れ
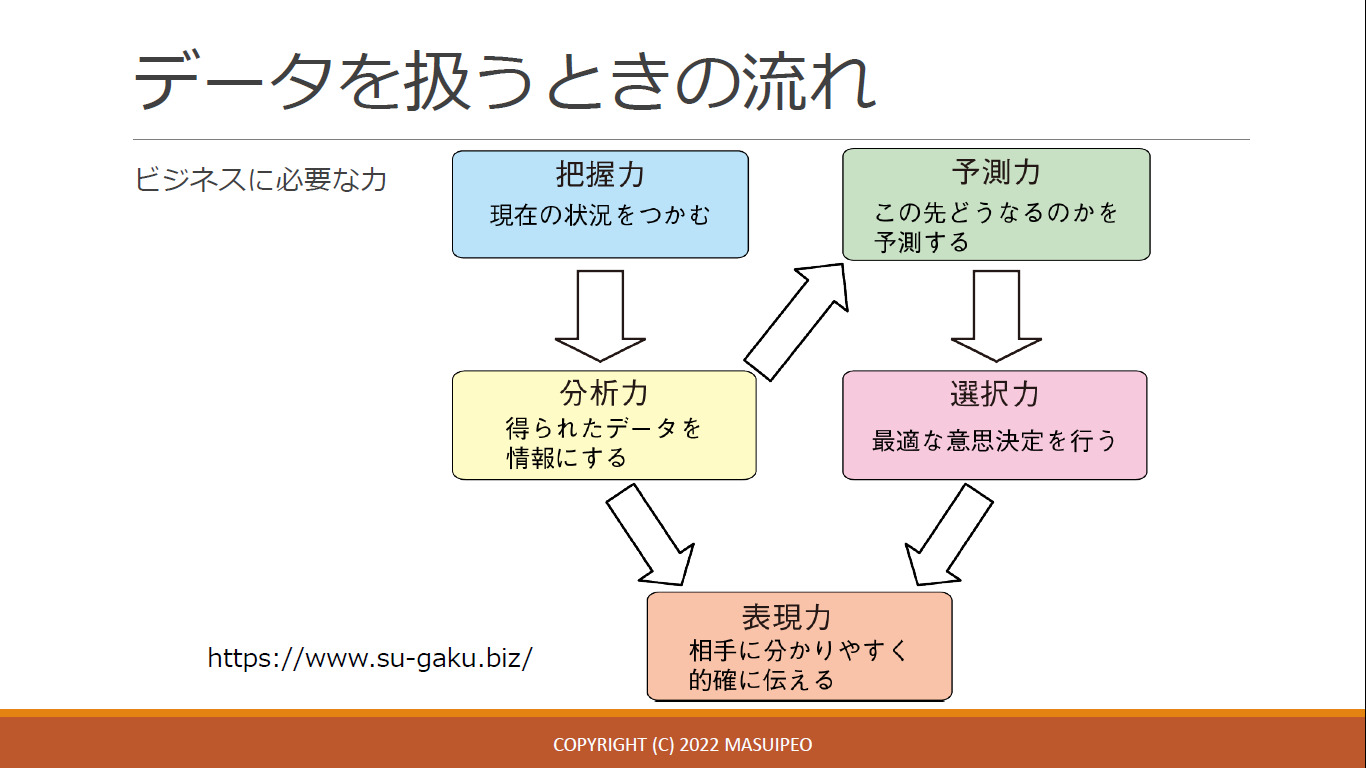
このデータ分析の流れに沿って、今日は説明が進みます。
データを把握する
まずは “データを把握する” というフェーズです。 まず把握にあたって注意すべきことから紹介いただきました。
- グラフは騙されやすい
- ex. 軸の情報が抜けている
- ex. 都合の良いところだけ比較している
- 作為的な集計
- ex. 割合がなく実数だけ 「 200 人が支持」
- ex. 実数だけで割合がない 「良い」という回答が前年比 2 倍
確かにグラフは騙されやすいですよね。 インターネットでもよく決算資料のグラフを注意されている光景を目にします。
続いて、データを把握するにあたって、よく使う指標を紹介いただきました。
- 代表値として 平均値/ 中央値/ 最頻値 のどれを使うか?
- 中央値は外れ値の影響を受けにくい
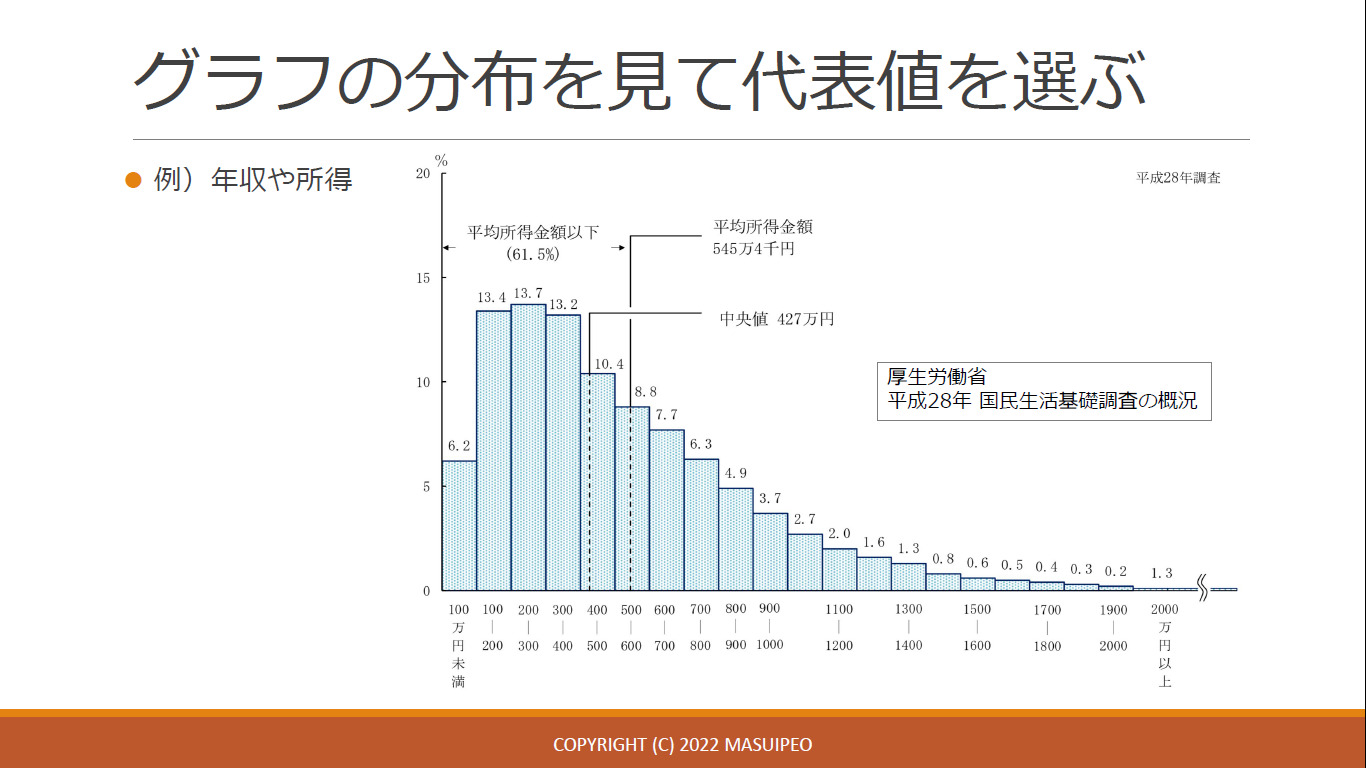
年収グラフを見ると中央値の特徴がわかりやすい - 分布の把握に適している
- ただし、中央値だけでは変化がわかりにくい
- 中央値は外れ値の影響を受けにくい
- 相関関係があるかどうか、相関係数で見よう
- 相関係数は Excel では CORREL 関数を使うと簡単に求められる
- -1 に近いと右肩下がり( = 負の相関)
- 1 に近いと右肩上がり( = 正の相関)
- ただし外れ値の影響を受ける
- 相関関係があるように見えて因果関係や擬似相関であることもある
- 因果関係: 原因と結果
- 擬似相関: 他の理由で相関があるように見える
- 相関係数は必ず散布図とセットで使う
- 曲線になる分布はわからず、あくまで直線的な関係がわかる
- 相関係数は Excel では CORREL 関数を使うと簡単に求められる
CORREL 関数が気になって見てみましたが、数式はわからなくとも操作方法は確かにめっちゃ簡単でした!
増井さん、便利情報、ありがとうございます!
データを分析する
さぁ、データを分析してみましょう! と、その前に … データの散らばり具合に注意しましょう、とのことでした。
- 平均や中央値ではデータの分布がわからない
- 平均からどれだけ離れているかを把握する
- 分散と偏差
- 分散は平均との差を 2 乗して平均 arrow_forward ただし単位が変わってしまう
- なので偏差は分散の平方根を取る
- 分散と標準偏差、単体の値では意味がない arrow_forward 比較で使う
- ex. 偏差値
- 分散と偏差
説明のあと、 Excel で分散( VAR 関数 )と標準偏差( STDEV 関数 )を試してみました。 複雑な数式を知らなくても Excel ならできました!
そして、いよいよ分析です! よく使う分析方法を解説いただきました。
- いろいろな項目を組みわせて件数や合計などを集計する
- ピボットテーブルをよく使う
- 複数回答があるものは正しく使えないことがある
クロス集計
ピボットテーブルならいちいち関数を適用せずとも、一回の操作でデータの傾向がわかるのが良いところです。
また、複数回答、複数の軸で使えるのが回帰分析です。
- 関数にして予測するときに使う
- Excel なら散布図から回帰直線を引ける(アドインで分析ツールを入れても実現できる)
- メニュー [挿入] から [散布図] を選択
- 散布図の [+] ボタンから “近似曲線の追加” のチェックボックスを on
- “近似曲線の追加” のメニューから “グラフに数式を表示する”
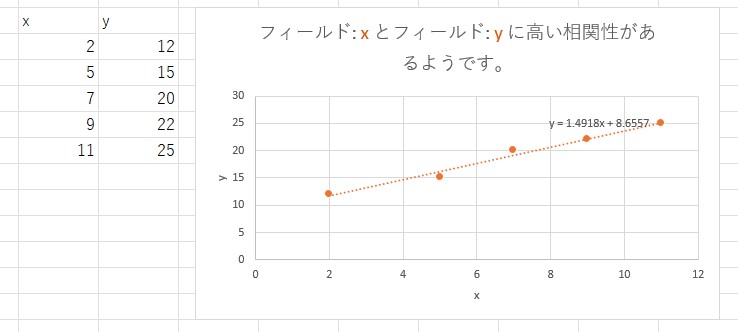
- ただし複数の変数( x 以外に説明変数がある)がある場合は使えない
回帰分析
Excel でここまで出来るの知らんかったです … 。 Excel 、ごめんな。
試しに過去の営業チームのコンタクト行動をした社数と売上のデータを入れてやってみると、相関あるやん!(当たり前) コンタクトした社数から予測できるやん!(当たり前)
データを表現する
分析したデータをもとに、データを表現する、説明するというフェーズです。
- 数値化すると客観的になる
- 「身長が高いです」より「身長は 188 cm です」の方がわかる
- 数値化の仕方
- 質的変数
- 名義尺度 分類するための数字 ex. 1: A 型, 2: B 型, 3: O 型, 4: AB 型 …
- 順序尺度 順番を割り当てたもの ex. 5: とても良い, 4: 良い, 3: 普通, 2: 悪い …
- 量的変数: 数値をそのまま計算できる。 間隔尺度と比例尺度の違いは 0 の扱い
- 間隔尺度 気温( 0 ℃ はある)
- 比例尺度 長さ( 0 cm は無い)
- 質的変数
- なぜ、数値化に種類があるのか? arrow_forward それによって表現が変わる
- ex. 順序尺度はその順序どおりに表現する
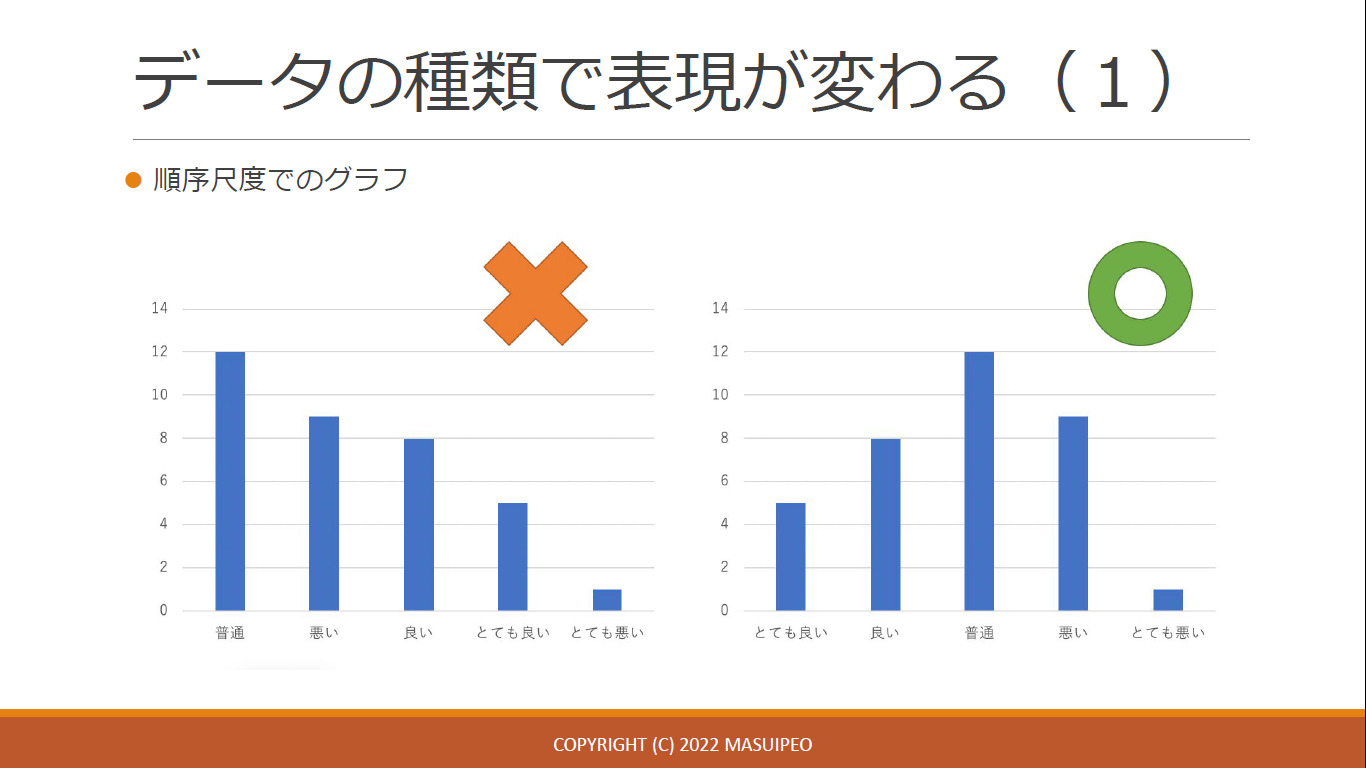
- ex. 質的変数の場合、棒グラフ。 量的変数の場合はヒストグラムが適している
- ex. 順序尺度はその順序どおりに表現する
では、練習してみましょう!

ヒント
- 区分ごとの応募数:
- 量を比較
- 年度ごとの応募数:
- 変化を表現したい
- 年代ごとの応募数:
- 割合を見たい
ただし、表現したら終わりではありません。 グラフだけでは何を伝えたいのかわからないからです。
これも練習してみましょう!

ヒント
パレート図で A 群 B 群 C 群にわけてみる( ABC 分析)
これまでの自分が説明不足すぎということを痛感しました。 ごめんな、これまで私が報告した方々。 まず、そもそもどんな図があるのかというところから修行し直します。
そんな私の気持ちを察していただいたのか、増井さんからいろいろな図と用途を紹介いただきました! さすがです !!
- 折れ線グラフの上手な使い方
- 様々な表現がある arrow_forward Google Chart API や Infogram などを見てみよう
- 箱ひげ図を使うと、 比較を多角的にできる
- 割合の変化は帯グラフが使える
ここでは詳細を割愛しますが、気になる方はぜひコースを受講してください!
データを選択する
データの把握、分析、表現という一連のサイクルに加えて、少し高度なテクニックということで、データの選択を紹介いただきました。 選択が直感派の私にはうってつけです!
代表的なデータを選択する方法を 3 つ紹介いただきました。
- 重み付け
- 重視する項目ごとに点数と重み付けを決めて計算する
- ex. スマートフォンを 機種 / デザイン / 性能 / 価格 のそれぞれで点数を決める
- 機種 / デザイン / 性能 / 価格 の重み付け( = 優先順位を決める)
- 点数 × 重み付けでスコアリング
- 優先順位の決め方
- 緊急度 / 重要度のマトリックス 4 象限で考える
- ただし重み付け or 点数を間違うと結果が変わる
- ロジカルにできるのが狩野分析法
- それがあるとどう思うか / それがないとどう思うか

- それがあるとどう思うか / それがないとどう思うか
- 重視する項目ごとに点数と重み付けを決めて計算する
- 主成分分析
- 変数が多くても特徴をつかみやすくなる
- ex. 野球選手の成績から特徴別に選手をまとめる
- 変数が多くても特徴をつかみやすくなる
- コレスポンデンス分析
- 沢山の次元があるデータでも特徴がわかる
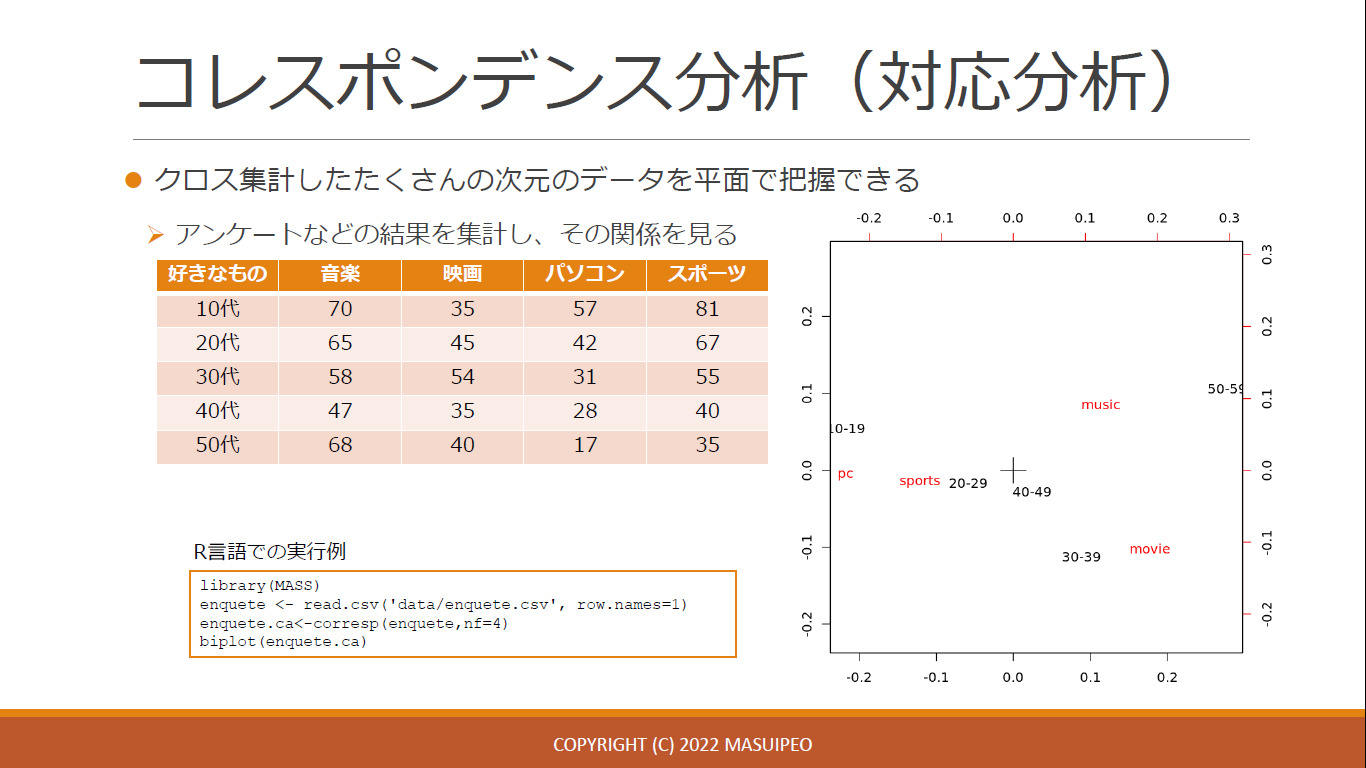
- 沢山の次元があるデータでも特徴がわかる
主成分分析やコレスポンデンス分析、初見でしたが、使いやすそうですよね! 様々な研修コースのアンケート結果をクロス集計してコレスポンデンス分析してみると、 “開発経験年数 10 年以上はマネジメント系コースの受講が多い” などわかるかも知れません!(しなくてもわかる)
データを予測する
最後はデータを予測するフェーズです。 これが今の時代だと一番やりたいことですね。
- 予想と予測は違う
- 予想: 根拠がない
- 予測: データによる根拠がある
- 遠い未来ほど予測は難しい
- 品質の良いデータがあると予測精度が上がる ↔ 大量でも質の悪いデータでは精度が下がる
- 値の範囲を推定する 区間推定 を使う( ex. 95 % がその範囲に入る)
- 予測する方法
- 移動平均: 区間をずらして平均を計算する ex. 株価
- 回帰分析: 関数に当てはめる ex. 標高と気温
- 確率: 期待値を使って起こる確率を求める ex. 宝くじの当選確率
予測方法も求めたいものに合わせて変えるのですね。 なるほど!
実際、この予測方法を練習してみます。 まずは回帰分析の応用である、フェルミ推定をやってみます!
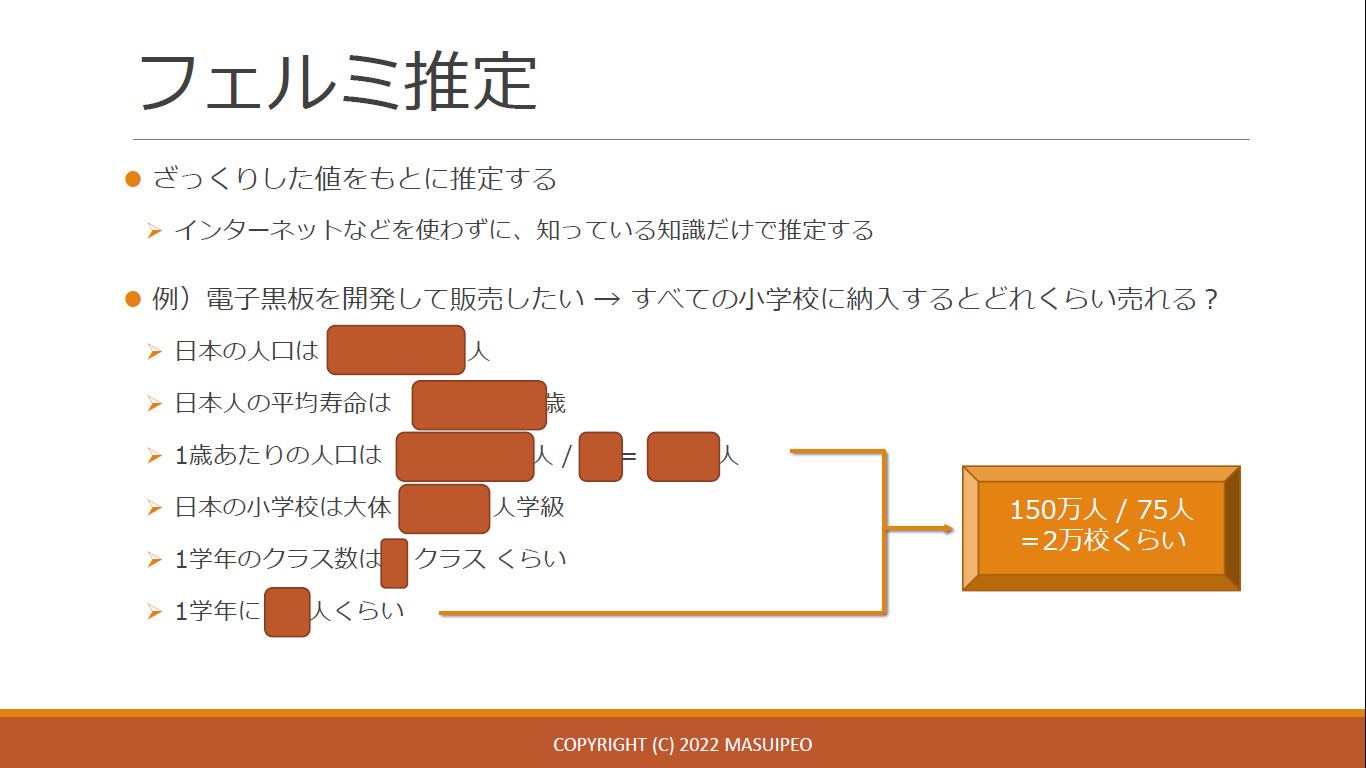
このほか、移動平均と確率についても練習してみたところで、このコースは修了しました。
まとめ
データ分析のフェーズ、把握、分析、表現、選択、予測、それぞれですること、使う方法( Excel の関数含む)、注意すべきことを解説いただきました。
そもそも統計をやってこなかった私が悪いのですが、それぞれの方法を学ぶごとに、「あ、これ、あのデータでやってみるといい感じになるかも !? 」のようなアイデアが沢山でてきました。 「無知は罪なり、知は空虚なり、英知持つもの英雄なり」と言いますので、ちゃんと知ったことを活かしてみます!
そして、 Excel 、これまで軽く見てきてごめんな。 これからは一緒にやっていくぞ Excel !
これまで統計に入門できなかった方や、これまでの Excel 観を変えたい方(いるのか?)にはとてもオススメのコースでした!
label SEカレッジを詳しく知りたいという方はこちらから !!

IT専門の定額制研修 月額 28,000 円 ~/ 1社 で IT研修 制度を導入できます。
年間 670 講座をほぼ毎日開催中!!

SEプラスにしかないコンテンツや、研修サービスの運営情報を発信しています。